Ответы
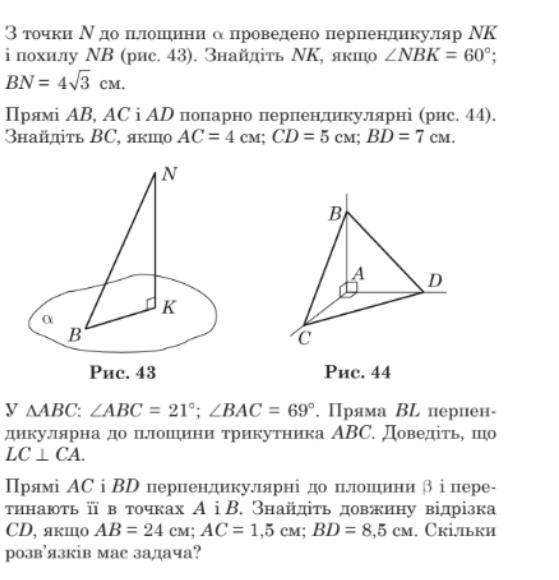
1. Якщо ∠NВК = 60° і ВN = 4√3 см, то NK можна знайти за допомогою формули для розрахунку сторони в рівносторонньому трикутнику, оскільки ∠NВК = 60°. Таким чином, NK = VN = BN = 4√3 см.
2. Якщо AC = 4 см, CD = 5 см, BD = 7 см і прямі АВ, АС і AD попарно перпендикулярні, то ВС можна знайти за допомогою Піфагорової теореми в просторовому трикутнику ABCD. ВС = √(AC² + BC²) = √(4² + 7²) = √65 см.
3. Якщо ∠АВС =21°, ∠BAC=69° і пряма BL перпендикулярна до площини трикутника АВС, то ∠L С А = 180° - ∠BAC - ∠АВС = 180° - 69° - 21° = 90°. Таким чином, ∠L С А є прямим кутом, що доводить, що пряма BL перпендикулярна до площини трикутника АВС.
4. Якщо AB=24см, AC=1,5см, BD=8,5см і прямі AC і BD перпендикулярні до площини в і перетинають її в точках A і B, то довжину відрізка CD можна знайти за допомогою формули для розрахунку довжини відрізка між двома точками в просторі. CD = √((AB - AC)² + BD²) = √((24 - 1,5)² + 8,5²) = √(22,5² + 8,5²) = √625 = 25 см. Задача має одне розв'язання.