Помогите пожалуйста)))в круге с центром О, изображенном на рисунке, проведено хорду АВ, которая равна радиусу круга. Через точки А и В, проведено касательные к кругу, которые пересекаются в точке С. найдите угол АСВ
Ответы
Ответ дал:
0
В круге с центром О, изображенном на рисунке, проведена хорда АВ, которая равна радиусу круга. Через точки А и В, проведены касательные к кругу, которые пересекаются в точке С. Найдите угол АСВ
----------------
Рисунок не дан, сделаем его - он несложный.
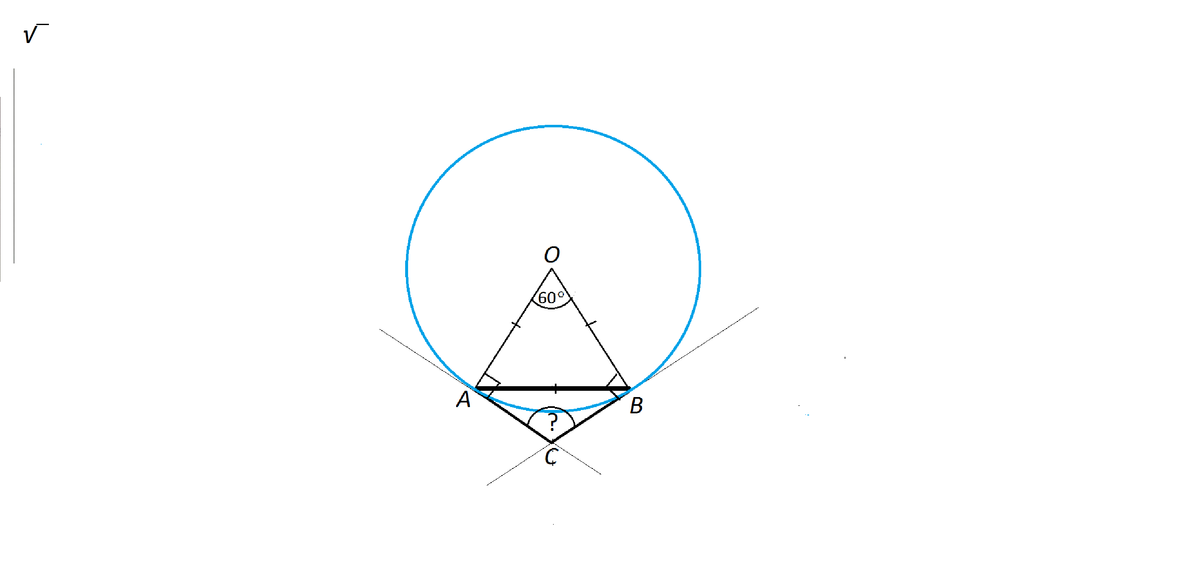
Соединим А и В с центром круга.
Так как хорда равна радиусу круга, получившийся треугольник АОВ - равносторонний,
и все углы в нем равны 60°.
Углы ОАС и ОВС - прямые по свойству радиуса и касательных.
Угол АОВ = 60°.
Сумма углов четырехугольника равна 360°.
Угол АСВ=360-ОАС - ОВС - АОВ=360-(2*90°-60°)=120°
----------------
Рисунок не дан, сделаем его - он несложный.
Соединим А и В с центром круга.
Так как хорда равна радиусу круга, получившийся треугольник АОВ - равносторонний,
и все углы в нем равны 60°.
Углы ОАС и ОВС - прямые по свойству радиуса и касательных.
Угол АОВ = 60°.
Сумма углов четырехугольника равна 360°.
Угол АСВ=360-ОАС - ОВС - АОВ=360-(2*90°-60°)=120°
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад