Question

C4

 
Длины сторон треугольника относятся как 2:3:4. В треугольнике
проведена биссектриса наименьшего угла. В каком отношении (считая от
вершины) эта биссектриса делится центром окружности, вписанной в
треугольник.

Answer 1

Центр вписанной окружности треугольника находится в точке пересечения биссектрис его углов. 
Точкой пересечения биссектрисы делятся в отношении суммы сторон треугольника, образующих угол, в котором проведена биссектриса, к третьей стороне.
Меньший угол треугольника расположен против меньшей стороны. 
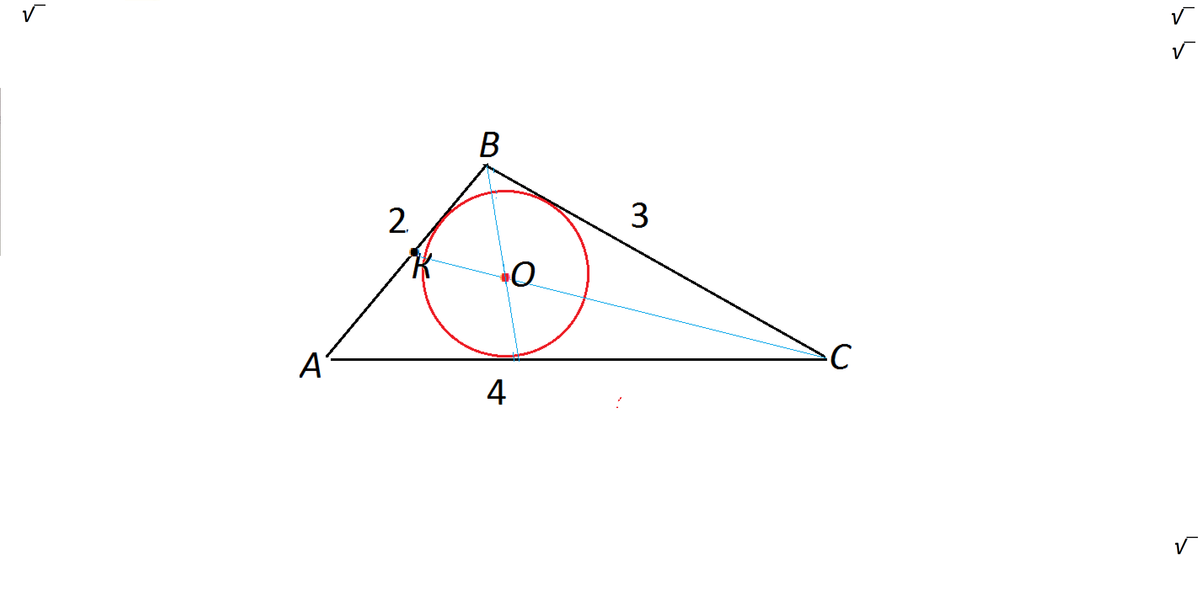
На приложенном рисунке это угол С. 
СО:ОК=(ВС+АС):АВ
 СО:ОК=(3+4):2=7:2