Question

Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежвщий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Заранее спасибо

Answer 1

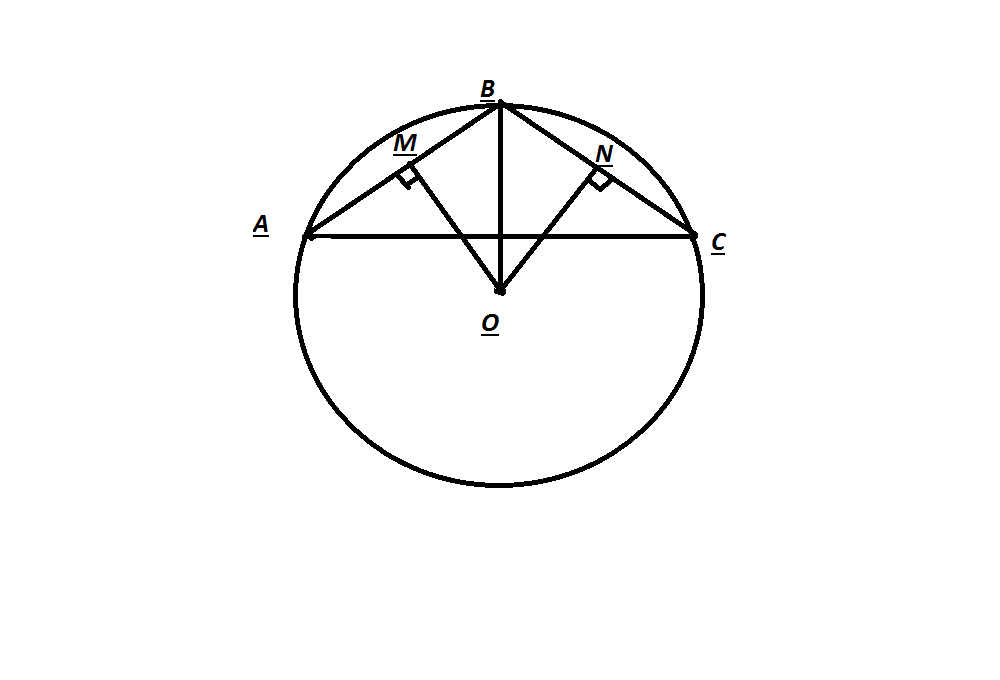
АB=BC=5. Угол B = 120'. Найди: d. 

Решение: 

Т.к. треугольник ABC равнобедренный, тогда угол BAC = углу BCA = 30'. 
BO-является высотой, биссектрисой и медианой и радиусом. 

Угол OBC = углу OBA =60' Центр описанной окружности треугольника находится на пересечении серединных перпендикуляров. Следовательно, CN=NB=BM=MA=2,5. 

Рассмотрим треугольник NOB: NO перпендикулярна BC.
Угол NBO=60', тогда угол BON=30'. А в прямоугольном треугольнике катет, лежащий против угла в 30', равен половине гипотенузы. Значит, BO=5. 
BO является радиусом окружности, тогда d=2r или  d=2*5=10. 

Ответ: d=10.