Question

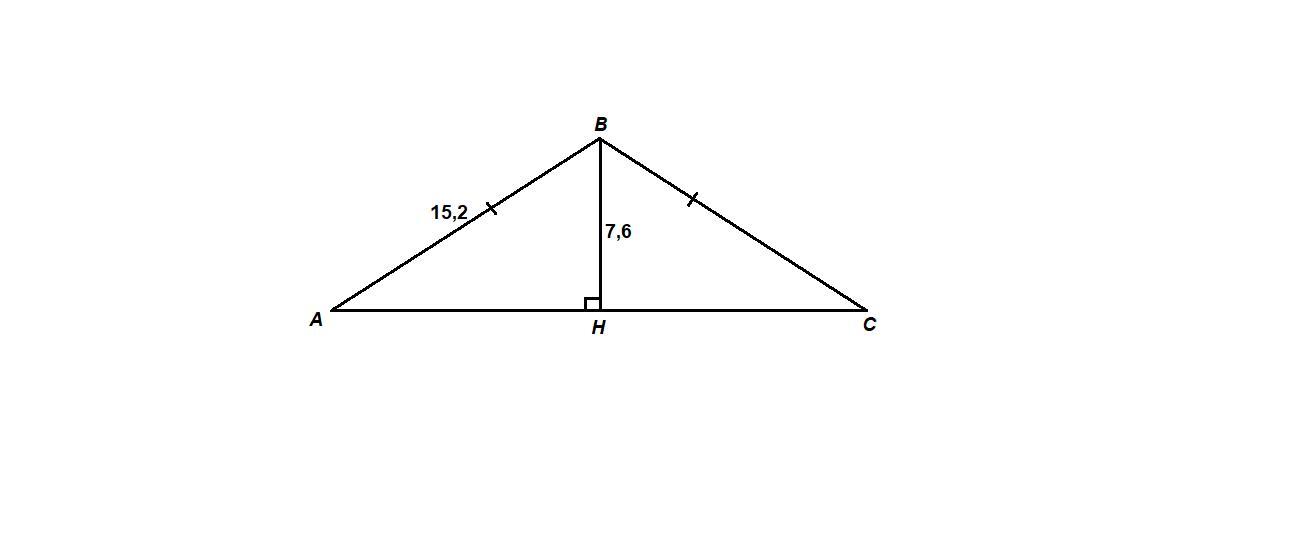
Высота, проведенная к основанию равнобедренного треугольника, равна 7.6 см, а боковая сторона треугольника равна 15.2 см. Найдите углы этого треугольника.

Answer 1

В прямоугольном треугольнике АВН катет ВН в два раза меньше гипотенузы АВ, значит, угол А равен 30°, поскольку в прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы. 
<ABH=180-<A-<BHA=180-30-90=60°
Поскольку в равнобедренном треугольнике высота, проведенная к основанию, является и биссектрисой, то 
<B=<ABH*2=60*2=120°
Углы при основании равнобедренного треугольника равны, значит
<C=<A=30°

Answer 2

Ответ:  30°, 30°, 120°.

Объяснение:

Рассмотрим прямоугольный ΔАВН:

АВ = 15,2 см, ВН = 7,6 см, значит

АВ = 2·ВН, тогда ВН - катет, лежащий против угла в 30°.

∠А = 30°.

Углы при основании равнобедренного треугольника равны, значит

∠С = ∠А = 30°

Сумма углов треугольника равна 180°, значит

∠В = 180° - (∠А + ∠С) = 180° - 2 · 30° = 120°