Question

Угол между двумя высотами ромба,проведенными из вершины тупого угла,равен 56градусов. Найдите величину острого угла ромба. 

Answer 1

ABCD - ромб. B и D - его тупые углы. Из вершины D проведем высоты DM и DN к сторонам АВ и ВС соответственно. Угол МDN=56 по условию. Треугольники MDB и NDB равны по катету и гипотенузе. Угол BDN=56/2=28, тогда угол DBN=90-28=62, следовательно, весь тупой угол ромба АВС=62*2=124. Острый угол BCD=(360-124*2)/2=56.

Вот так.

Answer 2

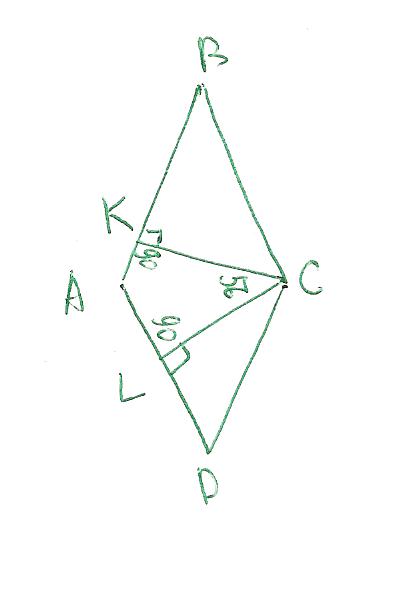
В четырехугольнике AKCL 360 градусов. Значит угол KAL равен 360-90-90-56=124. Это получается величина тупого угла. А их в ромбе 2, также как и острых, значит острый угол равен 360-2*124=56.

                                                       Ответ:56 градусов.