К прямой АВ проведены в разные полуплоскости перпендикуляры АМ и ВК. Отрезки МК и АВ пересекаются в точке О. Доказать, что треугольник АОМ=треугольнику ВОК, если известно, что АМ=ВК.
Ответы
Ответ дал:
0
По условию АМ и ВК - перпендикуляры. Две прямые, перпендикулярные к третьей, не пересекаются, значит
AMIIBK.
<AMK=<MKB как накрест лежащие углы при пересечении двух параллельных прямых АМ и ВК секущей МК.
<MAO=<OBK=90° по условию
АМ=ВК по условию
Значит, треугольники АОМ и ВОК равны по второму признаку равенства: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.
AMIIBK.
<AMK=<MKB как накрест лежащие углы при пересечении двух параллельных прямых АМ и ВК секущей МК.
<MAO=<OBK=90° по условию
АМ=ВК по условию
Значит, треугольники АОМ и ВОК равны по второму признаку равенства: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.
Приложения:
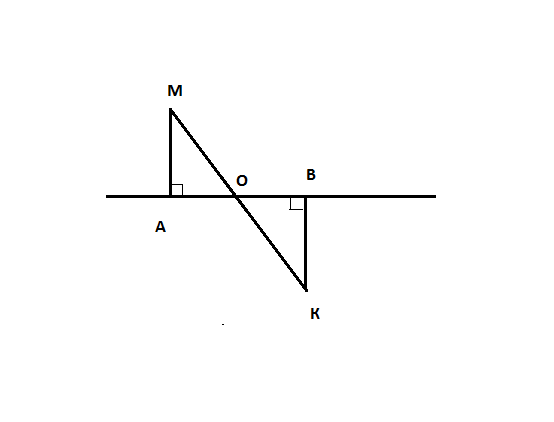
Ответ дал:
0
спасибо огромное, теперь все понятно
Ответ дал:
0
не мог бы ты помочь мне с задачей?
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад