Question

№1 

Пусть А - множество квадратов натуральных чисел, В - множество кубов натуральных чисел. Принадлежит ли: а) пересечению множеств А и В число 1; 4; 64; б) объединению множеств А и В число 16; 27; 64 ?

№2

Проиллюстрируйте с помощью кругов Эйлера соотношение между множествами А и В, где А - множество целых чисел, кратных 6, В - множество целых чисел, кратных 12. Какое множество является: а) пересечением множеств А и В; б) объединением множеств А и В ?

Решение нужно не из интернета. А реально решено самостоятельно. Буду очень благодарен. 

Answer 1

№ 1

а) Чтобы число принадлежало пересечению множеств А и В, оно должно принадлежать и множеству А, и множеству В.

1=1² ∈ А

1=1³ ∈ В

Следовательно 1 ∈ А∩В.

4=2² ∈ А

4=(∛4)³ ∉ В

Следовательно 4 ∉ А∩В.

64=8² ∈ А

64=4³ ∈ В

Следовательно 64 ∈ А∩В.

б) Число принадлежит объединению множеств А и В, если оно принадлежит либо множеству А, либо множеству В.

16=4² ∈ А ⇒ 16∈А∪В

64=8² ∈ А ⇒ 64∈А∪В

27=3³ ∈ В ⇒ 27∈А∪В

№ 2

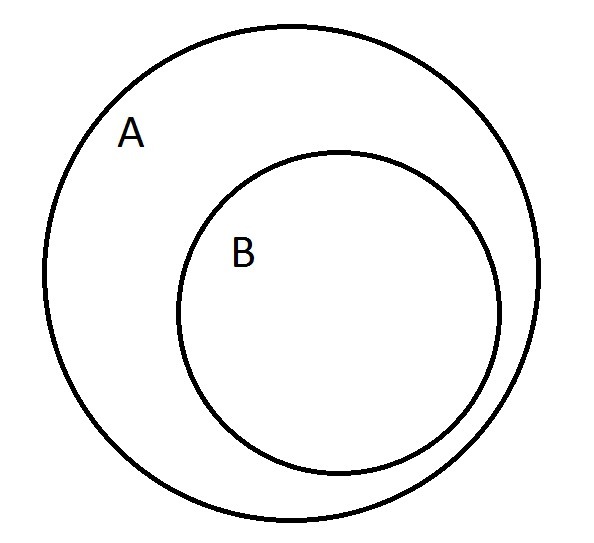
Рисунок в прикрепленном файле.

А - множество целых чисел, кратных 6.

В - множество целых чисел, кратных 12.

а) А∩В = В.

б) А∪В = А.