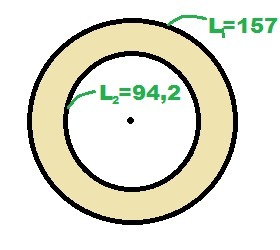
две окружности имеют общий центр,а длины их равны соответственно 157 и 94,2.Найдите площадь кольца,заключенного между этими окружностями
Ответы
Ответ дал:
0
L₁ = 2πR = 157 ⇒ 
L₂ = 2πr = 94,2 ⇒
Площадь кольца
S = S₁ - S₂ = πR² - πr² = π(R²-r²)

S ≈ 1256
L₂ = 2πr = 94,2 ⇒
Площадь кольца
S = S₁ - S₂ = πR² - πr² = π(R²-r²)
S ≈ 1256
Приложения:
Вас заинтересует
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад