Question

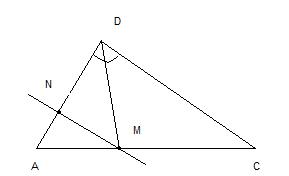
Отрезок DМ – биссектриса треугольника ADC.  Через точку М  проведена прямая, параллельная стороне  CD  и пересекающая сторону  DA  в точке  N.       Найдите углы треугольника   DMN,  если  ADC = 72. градуса

Answer 1

<NDM=<MDC=72/2=36°
<МDС=<NMD как накрест лежащие углы при пересечении двух параллельных прямых CD и MN секущей DM.
<NMD=36°
Зная, что сумма углов треугольника равна 180°, находим неизвестный угол MND треугольника DMN:
<MND=180-<NDM-<NMD=180-36*2=108°