Question

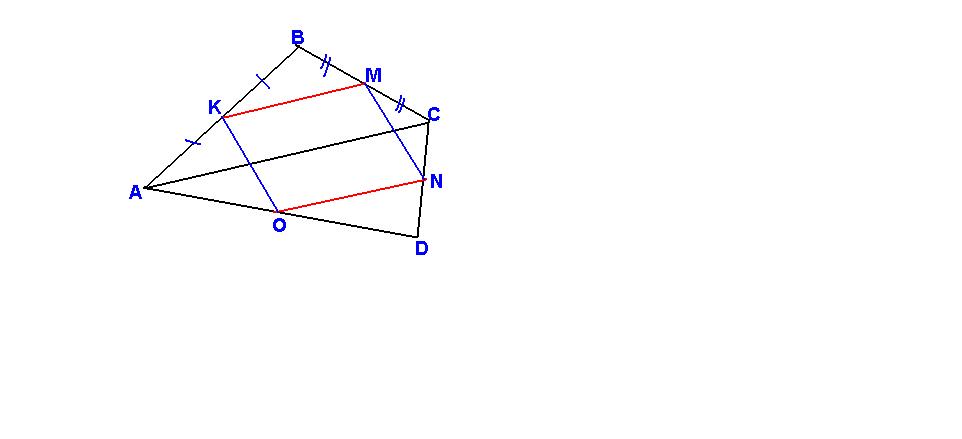
Докажите, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма.

Answer 1

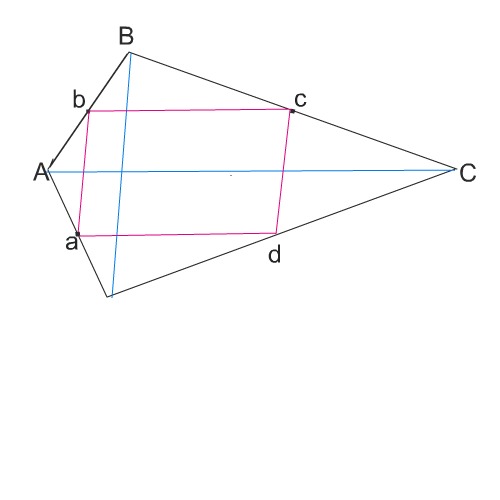
Проведем диагонали в этом четырехугольнике.

Получим четыре треугольника. (См. рисунок)

Если соединить середины четырехугольника, получим среднюю линию каждого из этих треугольников, причем эти средние линии попарно равны и параллельны, так как у пар треугольников с противоположными вершинами - общие основания. 

Четырехугольник, стороны которого попарно параллельны - параллелограмм. Ч.т.д.

Answer 2

 Смотри вложение.

КМ средняя линия треуг. АВС(по определению), тогда КМ = АС/2 и КМ параллельна АС

ON средняя линия треуг. ADC, значит ON = AC/2 и ON параллельна АС

Получаем, что KM=ON и KM параллельна ON(это признак!)Если две стороны четырехуг. равны и параллельны, то четырехуг. - параллелограмм.

Значит KMNO параллелограм.