Ответы
Ответ дал:
0
Дано:
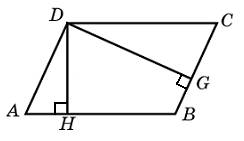
(рисунок внизу, токо у тебя без отрезка DG)
h(DH)=12 см
AD= 12 см
Найти:
sinB
Решение:
sinB=b/c
b-это один из катетов прямоугольного треугольника ADH
с- гипотенуза прямоугольного треугольника ADH
В данном случае ты знаешь катет a и гипотенузу. С помощью теоремы Пифагора находишь катет b





b=5
Теперь подставляешь в формулу синуса:
sinB = 5/13
А дальше сам посчитаешь )
(рисунок внизу, токо у тебя без отрезка DG)
h(DH)=12 см
AD= 12 см
Найти:
sinB
Решение:
sinB=b/c
b-это один из катетов прямоугольного треугольника ADH
с- гипотенуза прямоугольного треугольника ADH
В данном случае ты знаешь катет a и гипотенузу. С помощью теоремы Пифагора находишь катет b
b=5
Теперь подставляешь в формулу синуса:
sinB = 5/13
А дальше сам посчитаешь )
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад