Question

Докажите,что если биссектриса одного из внешних углов треугольника параллельна противоположной стороне треугольника,то этот треугольник равнобедренный.

Answer 1

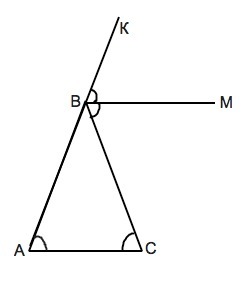
На рисунке приложения угол КВС –  внешний при вершине В. 

ВМ- биссектриса. 

ВМ║АС. 

ВС - секущая при параллельных ВМ и АС⇒

Накрестлежащие ∠МВС=∠ВСА  

и ∠КВМ=∠ВАС - соответственные. Но угол КВМ=МВС=ВСА. --

Угол ВСА=ВАС. 

Если углы при основании треугольника равны, то этот треугольник равнобедренный. ⇒

Треугольник АВС - равнобедренный. Доказано.