Ответы
Ответ дал:
0
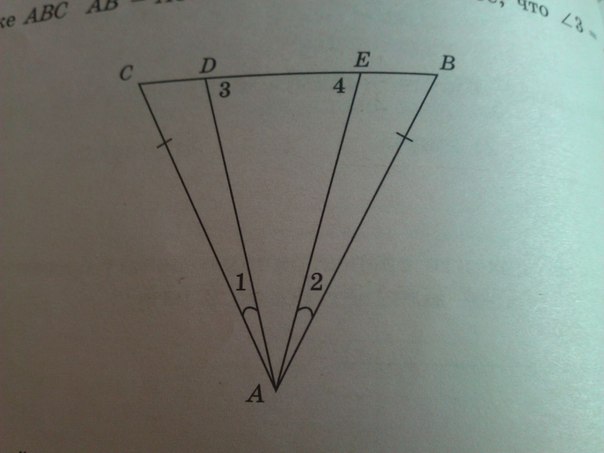
если треугольник равнобедренный, то В=С, угол 3=1+ С, как внешний для треуг АСД, аналогично, 4=2+В. Значит 3=4 как суммы соответственно равных углов.
Ответ дал:
0
Так как треугольник АВС равнобедренный АС= АВ, то углы при вершинах С и В равны.
Треугольники АDC и АЕВ равны по 2 признаку равенства треугольников.
(АD=AE, угол1=углу2, уголС=углуВ)
Значит треугольник АDЕ равнобедренный и углы при основании DЕ равны угол 3 = углу4.
Треугольники АDC и АЕВ равны по 2 признаку равенства треугольников.
(АD=AE, угол1=углу2, уголС=углуВ)
Значит треугольник АDЕ равнобедренный и углы при основании DЕ равны угол 3 = углу4.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад