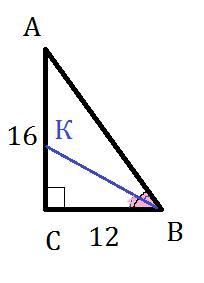
Катети прямокутного трикутника дорівнюють 12 см і 16 см. Знайти довжину бісектриси трикутника, що проведена з вершини більшого гострого кута.
Ответы
Ответ дал:
0
По теореме Пифагора
c^2=a^2+b^2
Пусть a=BC=12; b=AC=16
Тогда
c^2=12^2+16^2=144+256=400;
c=20
Больший острый угол лежит против большего катета, т.е это угол В.
Биссектриса BК делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
СК:КА=BС:AВ=12:20=3:5
CK=(3/5)KA
CK+KA=CA
(3/5)KA+KA=CA
(8/5)KA=16
KA=10
CK=6
По теореме Пифагора из прямоугольного треугольника СВК
BK²=BC²+KC²
BK²=12²+6²=144+36=180
BK=√180=√(36·5)=6√5
О т в е т. 6√5
Приложения:
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад
11 лет назад