Question

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM 10 см и BM 18 см.
Касательная к окружности описанной около треугольника проходящая через точку C пересекается с продолжением AB в точке D. найти CD ?  

Answer 1

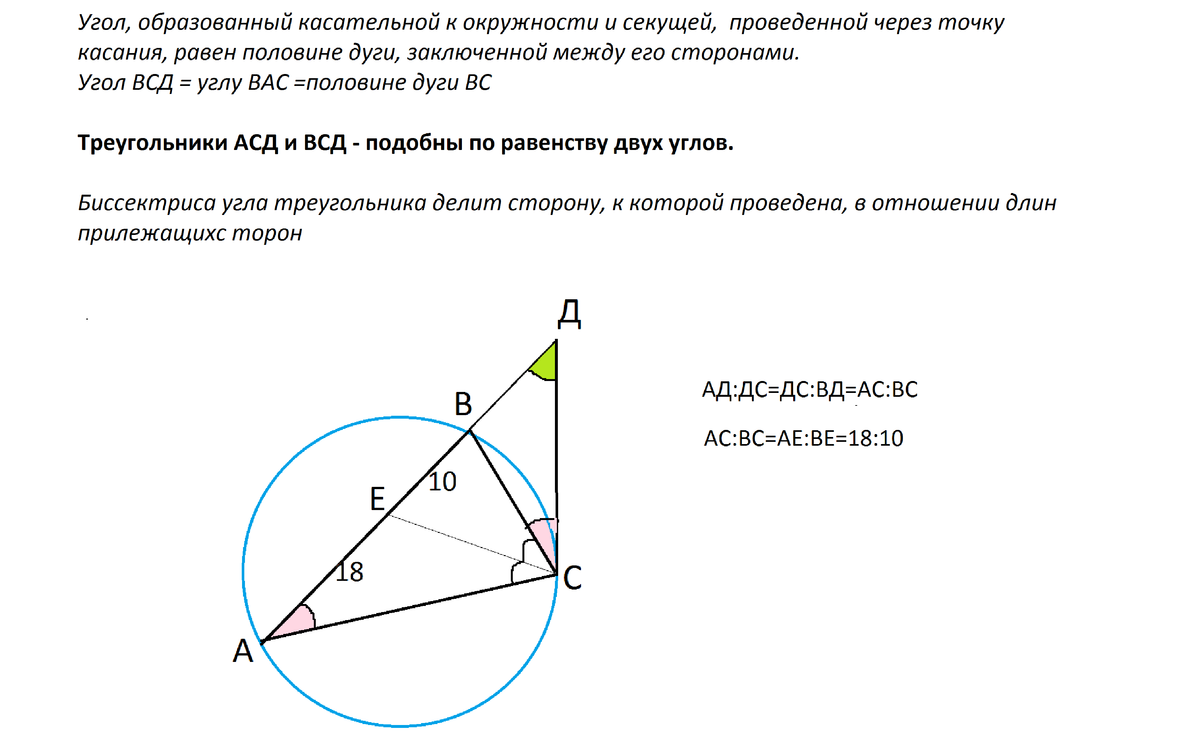
 СD - отрезок касательной.
Продолжение АВ = АD - секущая.
Рассмотрим рисунок, данный во вложении.
На секущей АД расположение обозначений идет в порядке:
А-Е-В-D, А и В - на окружности.  СЕ- биссектриса, АЕ=18, ВЕ=10
Угол, образованный касательной ДС к окружности и секущей ВС, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Следовательно, угол DАС=углу ВСD.
В треугольниках АDС и ВDС по два равных угла:
угол D - общий, угол ВСD =углу DАС, следовательно, они подобны. 
В подобных треугольниках соответственные стороны лежат против равных углов.
Найдем отношение сторон в треугольниках.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Следовательно, АС:ВС=18:10
Из подобия треугольников ВDС и СDА 
DС:ВD=18/10
DС=18*ВD/10
Пусть ВD - внешняя часть секущей АD - равна х
Тогда DС=18х/10
и АD=АЕ+ВЕ+х=28+х
Квадрат длины  отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть. 
 DС²=ВД*АD
(18х/10)²=х(28+х)
324х²:100=28х+х²
Домножив обе части уравнения на 100, получим:
324х²=2800х+100х²
224х²=2800х 
х=2800х:224х
х=12,5 см
DС=12,5*(18/10)=22,5 см
 --------------
[email protected]