Question

треугольник АВС вписан в окружность угол С = 45 из точки М расположенной вне круга проведены касательные МР и МТ касающиеся окружности в точках А и В соответственно
докажите что ОАМВ - квадрат где О - центр окружности

Answer 1

Касательные MP и MT к окружности перпендикулярны к радиусам OA и OB, проведенными в точках касания, т.е. углы А и В равны 90°

Отрезки МА и МВ касательных  MP и MT к окружности, проведенных из одной точки М, равны МА = МВ

Вписанный угол <С =45° равен половине центрального угла < О, опирающегося на ту же дугу АВ, значит угол   < О=90°.

Таким образом имеем углы А, В, О равны 90°   , значит и угол М =  90°  , стороны OA = OB (радиусы), тогда и стороны МА =МВ= OA = OB из чего следует, что ОАМВ - квадрат , что и требовалось доказать.

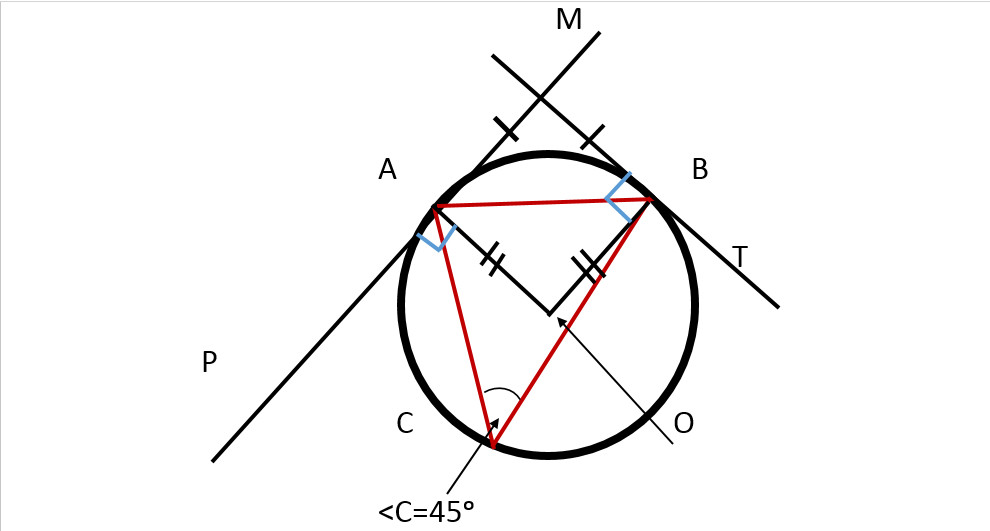
Смотри рисунок.