Ответы
Ответ дал:
0
Решение на фото 1, 2
Продолжение решения на фото 3
Ответ:
![frac{1}{9} < x < frac{1}{3}, ; frac{1}{ sqrt[3]{9} } leq x<1, ; x geq 3 \ \
(frac{1}{9}; frac{1}{3}) vee [frac{1}{ sqrt[3]{9}};1) vee [3;+besk). frac{1}{9} < x < frac{1}{3}, ; frac{1}{ sqrt[3]{9} } leq x<1, ; x geq 3 \ \
(frac{1}{9}; frac{1}{3}) vee [frac{1}{ sqrt[3]{9}};1) vee [3;+besk).](https://tex.z-dn.net/?f=frac%7B1%7D%7B9%7D+%26lt%3B+x+%26lt%3B++frac%7B1%7D%7B3%7D%2C+%3B++frac%7B1%7D%7B+sqrt%5B3%5D%7B9%7D+%7D++leq+x%26lt%3B1%2C+%3B+x+geq+3+%5C+%5C%0A%28frac%7B1%7D%7B9%7D%3B+frac%7B1%7D%7B3%7D%29+vee+%5Bfrac%7B1%7D%7B+sqrt%5B3%5D%7B9%7D%7D%3B1%29+vee+%5B3%3B%2Bbesk%29.)
Продолжение решения на фото 3
Ответ:
Приложения:
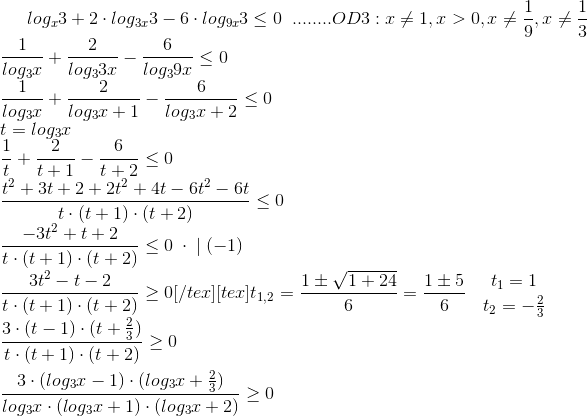


Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад