Найти диагональ и боковую сторону равнобочной трапеции с основаниями 20 см и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
Ответы
Ответ дал:
0
Решение:
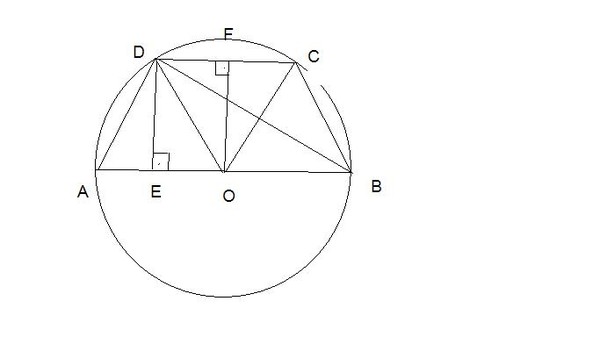
AO=OB=OC=OD=10 это радиус описанной окружности
OF=корень (DO^2-DF^2)=8
DF=CF=EO=6
OF=DE=8
AE=AO-EO=4
AD=BC
AD=sqrt (AE^2+DE^2)=4*sqrt (5)
AC=BD
BD=sqrt (DE^2+(EO+OB)^2)=8*sqrt (5)
p/s
sqrt - корень
AO=OB=OC=OD=10 это радиус описанной окружности
OF=корень (DO^2-DF^2)=8
DF=CF=EO=6
OF=DE=8
AE=AO-EO=4
AD=BC
AD=sqrt (AE^2+DE^2)=4*sqrt (5)
AC=BD
BD=sqrt (DE^2+(EO+OB)^2)=8*sqrt (5)
p/s
sqrt - корень
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад