Ответы
Ответ дал:
0
Ромб является частным случаем параллелограмма, значит его площадь как параллелограмма равна: S=ah, где a - сторона ромба, h - его высота.
С другой стороны, площадь ромба равна половине произведения его диагоналей.
Диагонали ромба перпендикулярны и пересекаются в точке, делящей их пополам.
Значит образуется прямоугольный треугольник. В нашем случае с гипотенузой 10 и катетом 6
Тогда половина второй диагонали ромба равна:
Значит вторая диагональ равна 8*2=16
S=(16*12)/2=96
h=S/a=96/10=9,6
Ответ дал:
0
Решение:
По формуле: S=ah, где a-сторона ромба, h-высота.
По рисунку видно,что половина диагонали равна 6 см.
Тогда половина второй диагонали ромба равна: см
Значит вторая диагональ равна 8*2=16см
S=(16*12)/2=96см
Значит h=S/a=96/10=9,6см
Ответ:9,6см
Приложения:
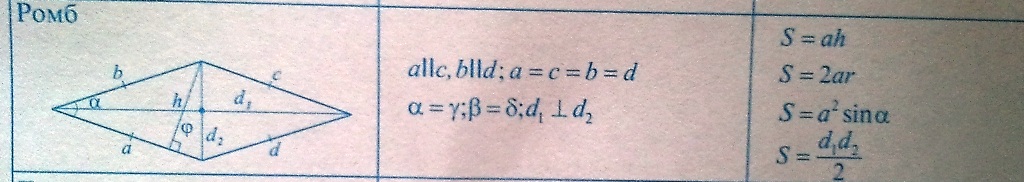
Вас заинтересует
2 года назад
2 года назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад