Вне окружности радиуса К взята точка А, из которой проведены две секущие, одна — проходящая через центр, а другая — на расстоянии К/2 от центра. Найти площадь части круга, расположенной между этими секущими.
Ответы
Ответ дал:
0
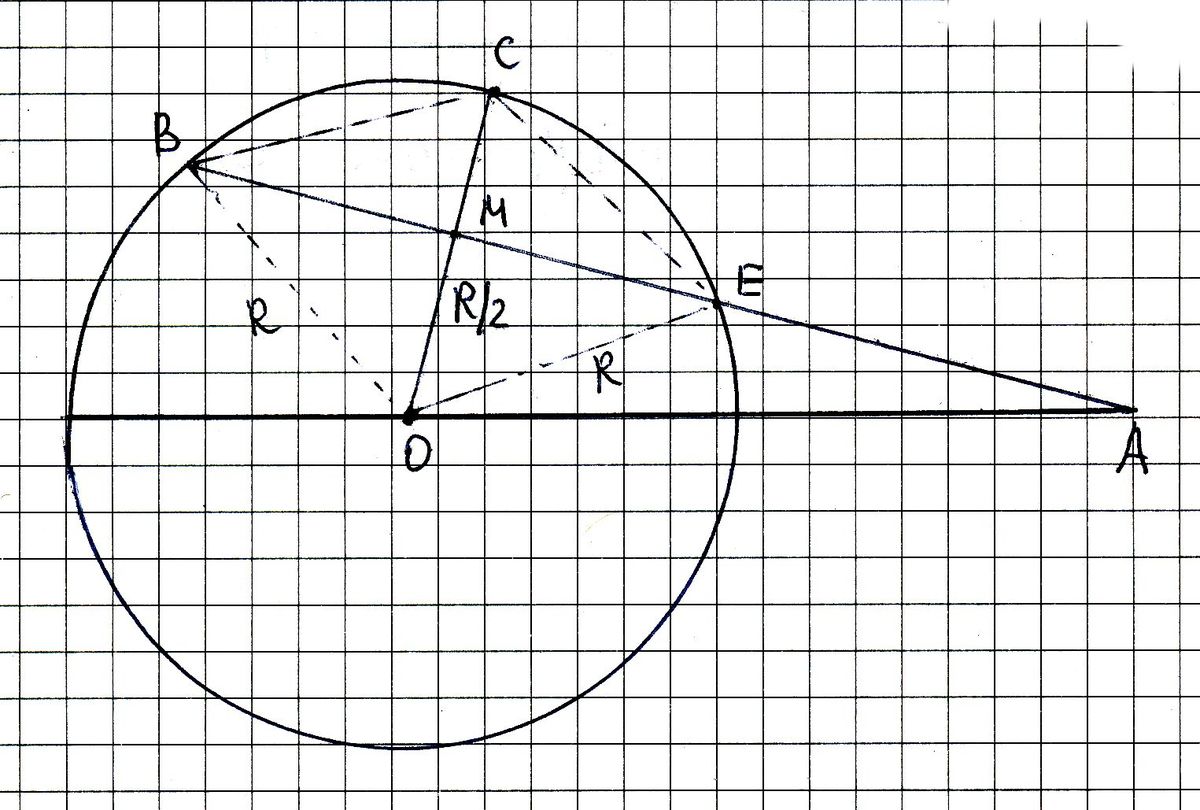
См. чертеж.
ОС перпендикулярно АВ, ОМ = ОС/2, поэтому ОВСЕ - ромб. Причем у этого ромба меньшая диагональ равна радиусу.
Площадь треугольника ОВЕ Sobe = R^2*корень(3)/4;
Угол ВОЕ = 2*pi/3; Площадь кругового сектора ОВСЕ =S/3; S = pi*R^2; площадь сегмента ВСЕ между дугой ВСЕ и хордой ВЕ равна S/3 - Sobe; искомая площадь равна S/2 - (S/3 - Sobe) = S/6 + Sobe = pi*R^2/6 + R^2*корень(3)/4 =
= R^2*(pi/6 + корень(3)/4);
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад