Question

В равнобедренной трапеции диагонали являются биссектрисами тупых углов и в точке пересечения делятся в отношении 13:3, считая от вершин острых углов. Найдите площадь трапеции, если ее высота=24 см

Answer 1

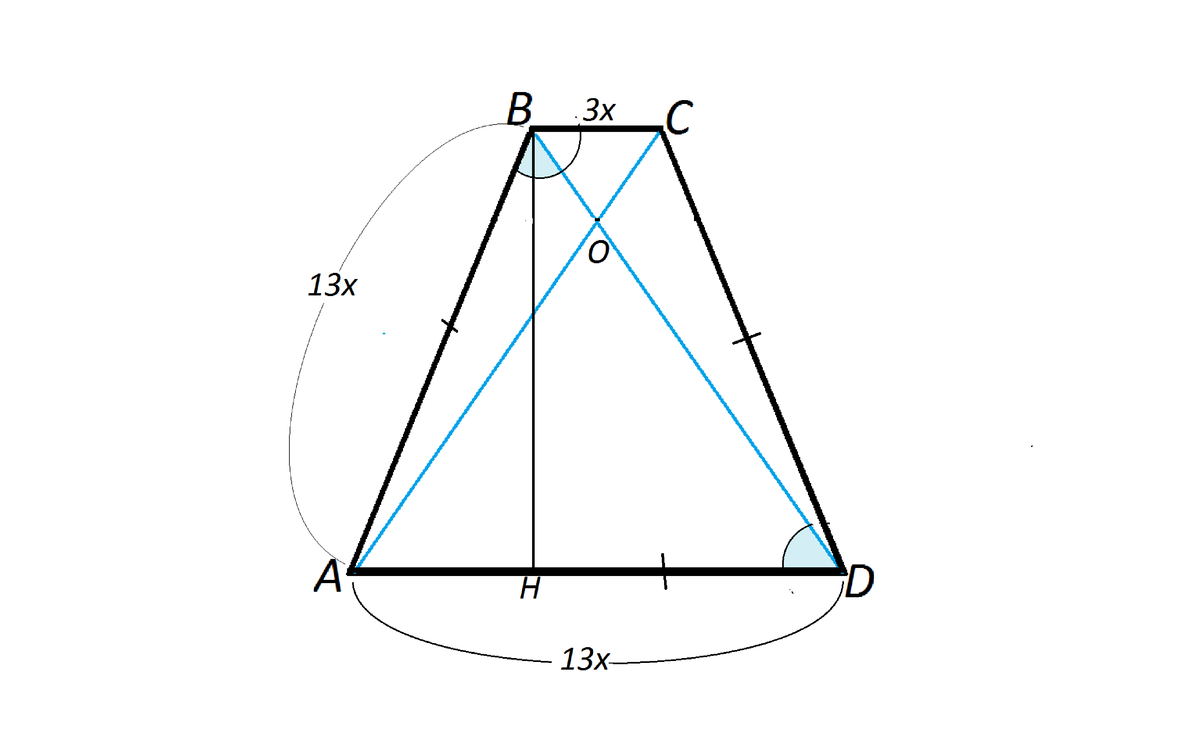
Пусть дана трапеция АВСD.
Диагонали трапеции  делят ее на 4 треугольника, из которых два подобны. 
△АОD подобен △ВОС. 
Отношение АО:ОС=13:3 ⇒
АD:ВС=13:3
∠СВD=∠ВDА по свойству углов при параллельных прямых и секущей
Но ВD - биссектриса ∠АВС  ⇒
∠СВD=∠АВD, ⇒
∠ВDА=∠АВD. 
△АВD - равнобедренный с равными углами при основании ВD и равными сторонами АВ=АD  
Пусть коэффициент отношения оснований будет х.
Тогда ВС:АD=3х:13х
АВ=АD=13х
Опустим высоту ВН на АD
Треугольник АВН - прямоугольный. 
АН=(АD-ВС):2=5х
АВ²-АН²=ВН²
169х²-25х²=576
144х²=576
х²=4
х=2 см
ВС=2*3=6 см
АD=2*13=26 см
Площадь трапеции равна произведению высоты на полусумму оснований:
S ABCD= BH(BC+AD):2=24*16=384 см²
----
[email protected]