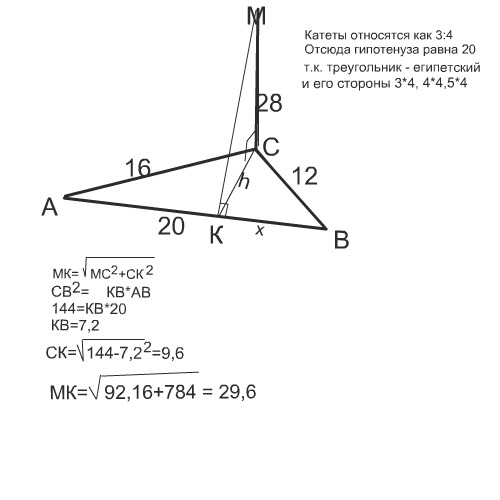
Катеты прямоугольного треуголиника ABC равны 12см и 16см.Из вершины прямого угла C проведен к плоскости треугольника перпендикуляр CM,равный 28см.Найдите расстояние от точки M до гепотенузы
Ответы
Ответ дал:
0
Гипотенуза треугольника АС = √16²+12²=√400= 20см
Проекцией искомой линии на плоскость является высота тр-а АВС, опущенная на гипотенузу. Из условия подобия тр-ков напишем пропорцию: h/16=12/20
h=12*16/20 = 9,6см
Расстояние от точки M до гепотенузы MD = √9,6²+28²= 29,6 cм
Ответ дал:
0
Данный в задаче треугольник - египетский с соотношением сторон 3:4:5
Вспомним, что
В прямоугольном треугольнике справедливы следующие соотношения:
1) h² = a1 · b1;
2) b² = b1 · c;
3) a² = a1 · c,
где b1 и a1 - проекции катетов b и a на гипотенузу с, h - высота треугольника.
Решение - во вложении.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад