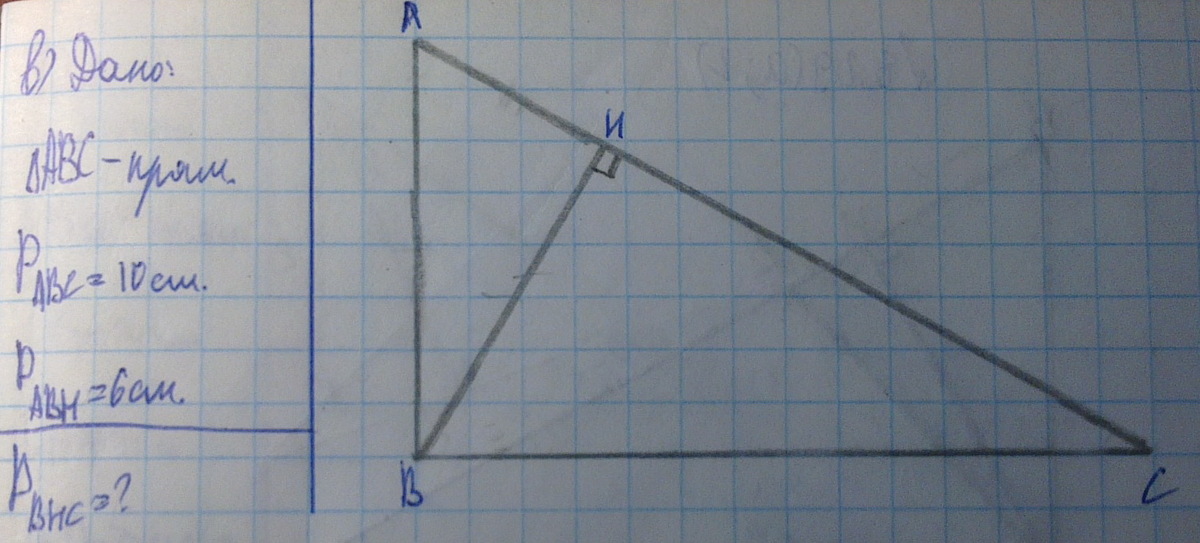
Помогите!!! Есть рисунок!!!! Прямоугольный треугольник, периметр которого равен 10, делится высотой, опущенной на гипотенузу, на два треугольника. Периметр одного, из которых равен 6. Найдите периметр второго треугольника.
Приложения:
Ответы
Ответ дал:
0
Обозначим стороны треугольников х, у,z, и высоту h (смотри рисунок). Далее исходим из того, что высота h проведённая к гипотенузе, делит прямоугольный треугольник на три подобных треугольника АВС, АВН и ВНС, а также, что отношение периметров подобных треугольников равно отношению сходственных сторон. Окончательный ответ Рвнс=8.
Приложения:
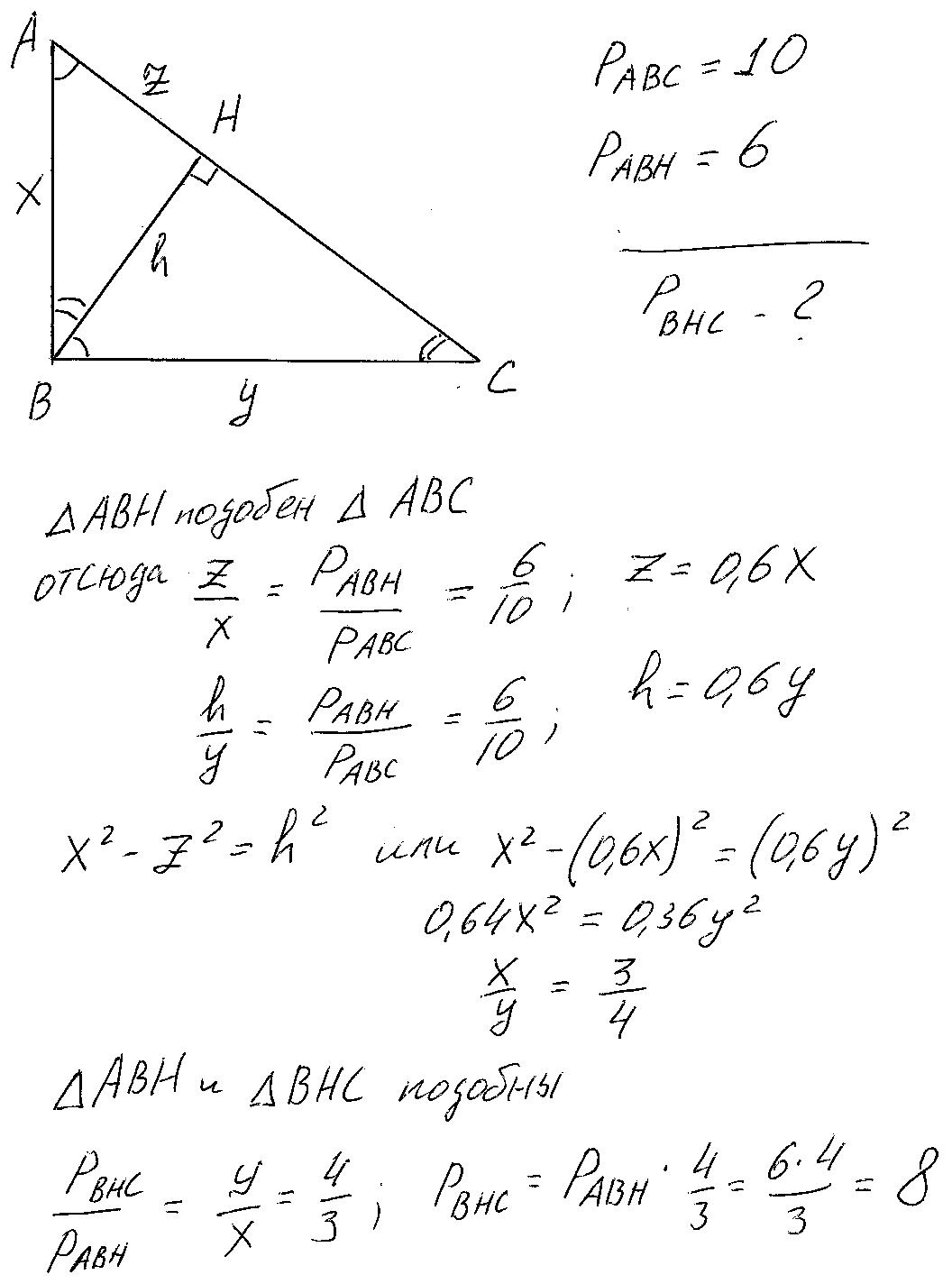
Вас заинтересует
8 лет назад
11 лет назад
11 лет назад