Question

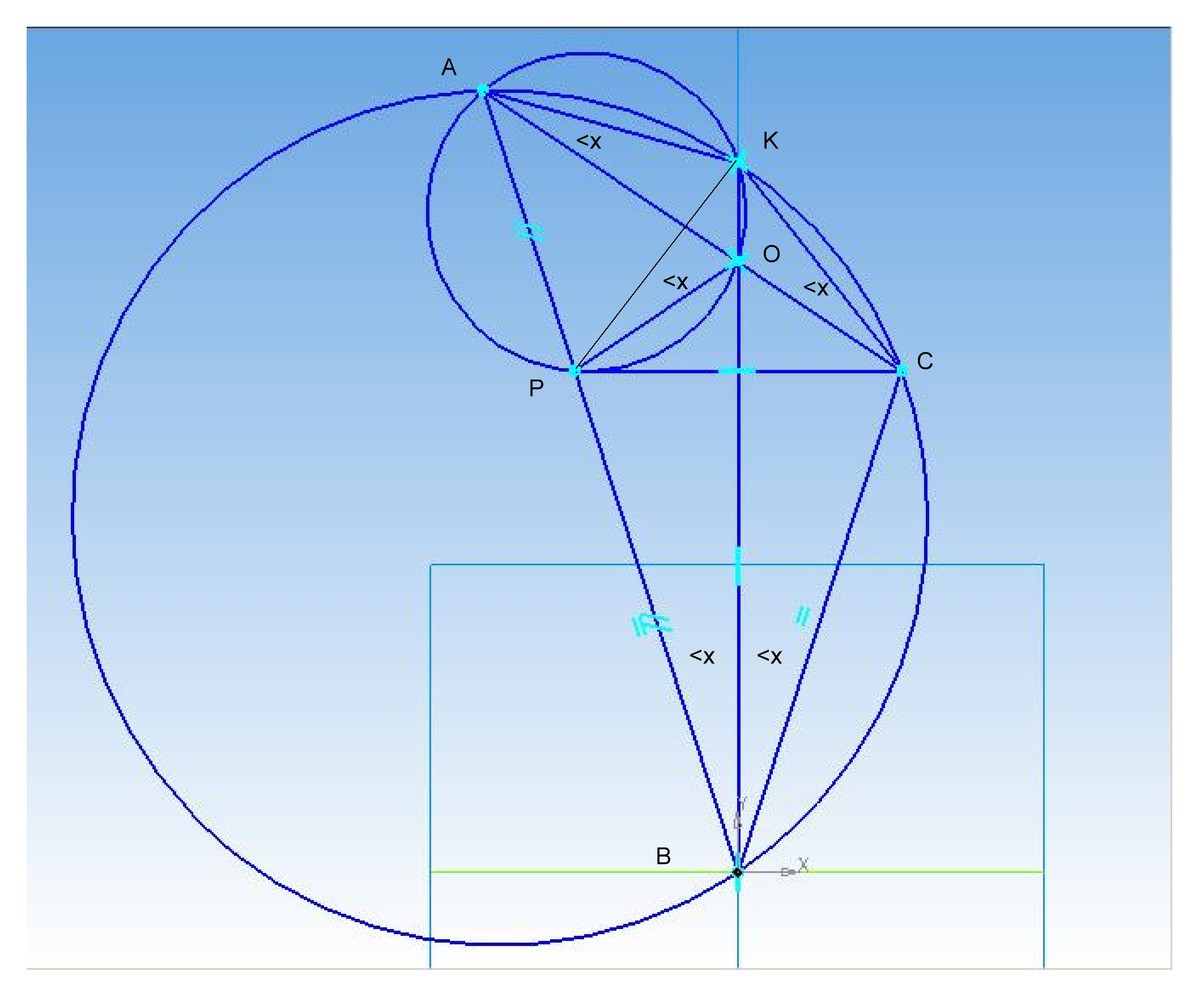
В треугольнике ABC сторона AB  больше стороны  BC ,  на стороне  AB отмечена точка P так,что PB=BC . Биссектриса BO пересекает описанную возле треугольника ABC окружность в точке K
Доказать,что точки A,K,O,P лежат на одной окружности 

Answer 1

пусть <ABK = <x
<ACK = <x - так как опираются на ту же дугу окружности АК что и <ABK = <x
<КВС = <x - так как ВО - биссектриса
<КАС = <x - так как опираются на ту же дугу окружности КС что и <КВС = <x
<КАО = <КАС=<x
так как BP = PC и BO - биссектриса, то РСВ - равнобедренный,
значит ВО - серединный перпендикуляр
значит РСК - равнобедренный и РСО - равнобедренный,
значит <КРО = <КСО
так как <КСО =<АСК = <x
значит <КРО = <x

и наконец
так как в 4-угольнике АКОР
<КАО = <x  и <КРО = <x, значит точки А и Р лежат на некой кривой, из которой отрезок КО виден под одинаковым углом
геометрическим местом точек, из которых данный отрезок КО виден под одним и тем же углом является дуга окружности, проходящей через концы отрезка КО
доказано, что точки АКОР лежат на одной окружности

Answer 2

на здоровье
у вас интересные и что немаловажно дорогие задачи )
обращайтесь