Ответы
Ответ дал:
0
cos10x Разложил по формуле суммы косинусов,1 появилась по основному тригонометрическому тождеству.
Приложения:
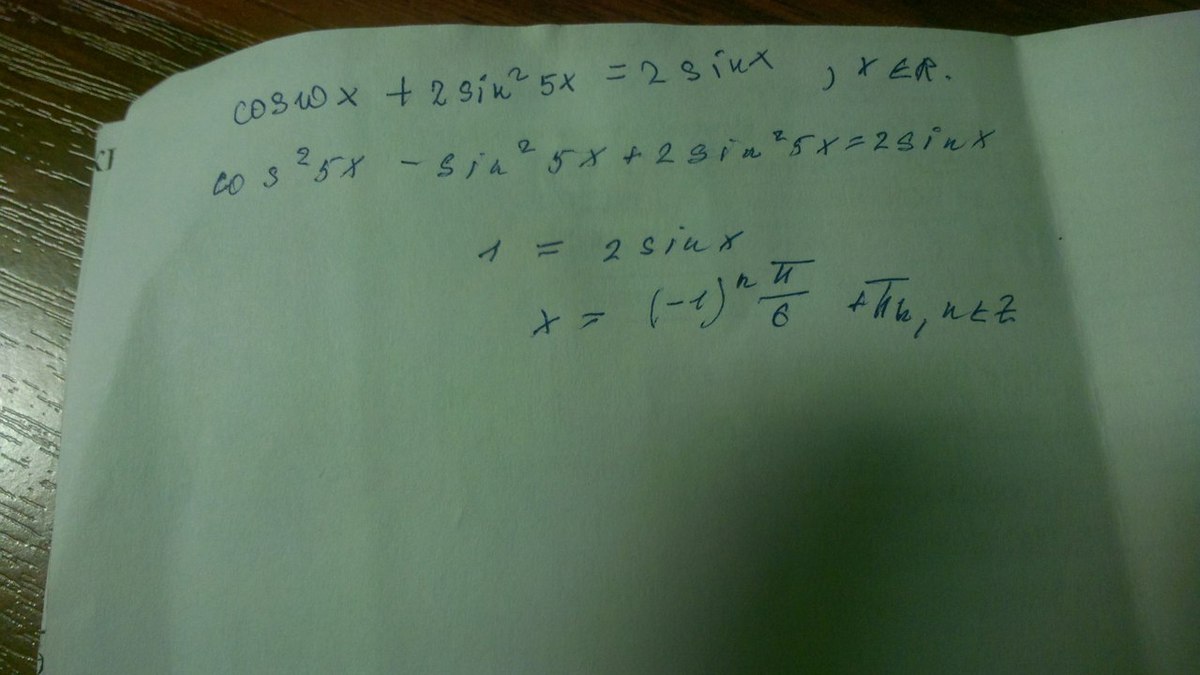
Ответ дал:
0
Приложения:
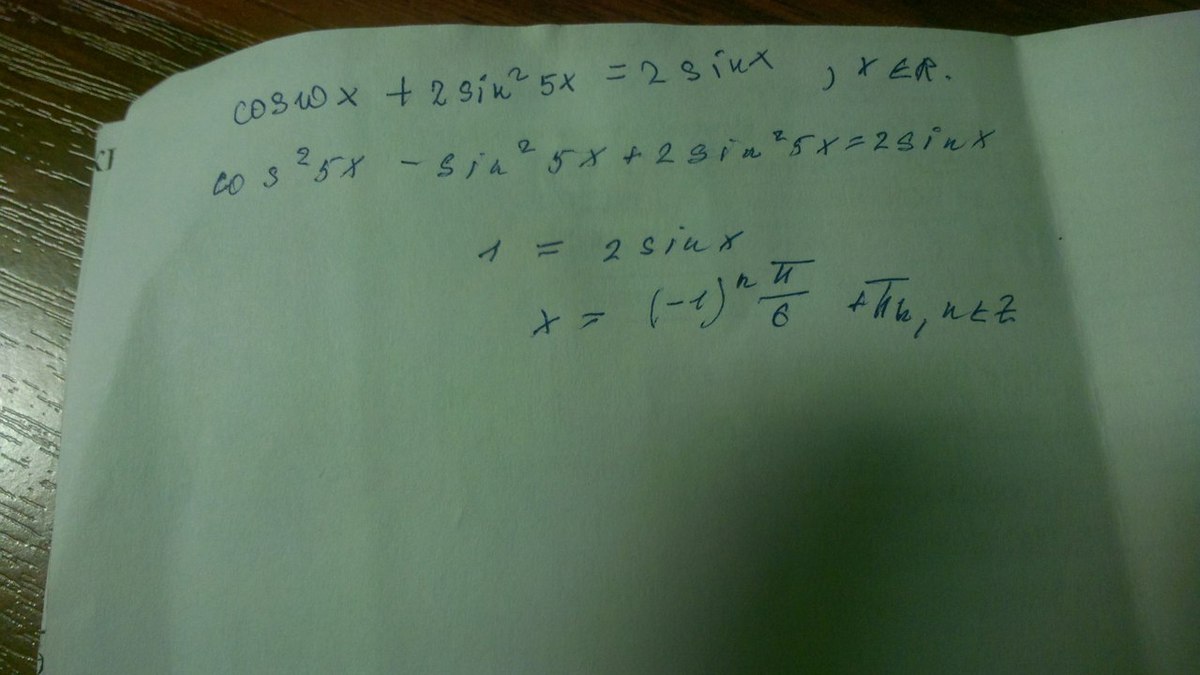
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад