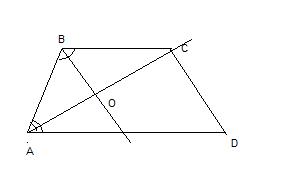
биссектрисы углов А и В выпуклого четырехугольника АВСД пересекаются в точке О. докажите, что угол АОВ равен 1/2 (С+Д)
Ответы
Ответ дал:
0
Рассмотрим треугольник АОВ. Зная, что сумма углов треугольника равна 180°, запишем:
<AOB=180-<BAO-<ABO=180-A:2-B:2=180-1/2(A+B)
Зная, что сумма углов выпуклого 4-угольника равна 360°, для углов А и В запишем:
<A+<B=360-<C-<D
В выражение для угла АОВ подставим значение суммы <A+<B:
<AOB=180-1/2(A+B)=180-1/2(360-C-D)=180-180+1/2C+1/2D=1/2C+1/2D=1/2(C+D)
<AOB=180-<BAO-<ABO=180-A:2-B:2=180-1/2(A+B)
Зная, что сумма углов выпуклого 4-угольника равна 360°, для углов А и В запишем:
<A+<B=360-<C-<D
В выражение для угла АОВ подставим значение суммы <A+<B:
<AOB=180-1/2(A+B)=180-1/2(360-C-D)=180-180+1/2C+1/2D=1/2C+1/2D=1/2(C+D)
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад