Question

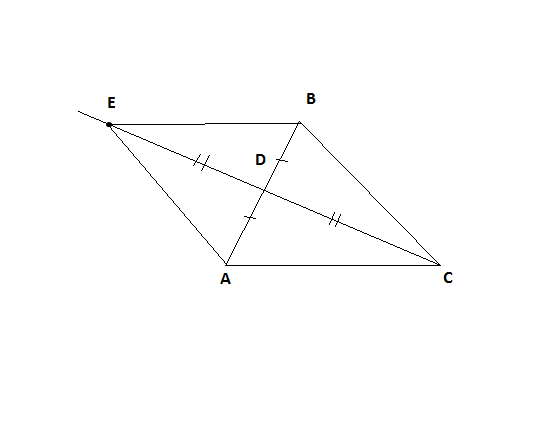
Дан треугольник ABC. На продолжении его медианы CD отложен отрезок DE=CD. Докажите равенство треугольников BAE и ABC.

Answer 1

Треугольники BDE и ADC равны по первому признаку равенства треугольников -по двум сторонам и углу между ними: BD=AD, DE=DC по условию, углы BDE и ADC равны как вертикальные углы.
Треугольники ADE и BDC равны также по двум сторонам и углу между ними: BD=AD, DE=DC по условию, углы ADE и BDC равны как вертикальные.  
Значит треугольник ВАЕ, состоящий из треугольников BDE и ADE, равен треугольнику АВC, состоящему из треугольников BDC и ADC.