Question

Математика - ЕГЭ - B6

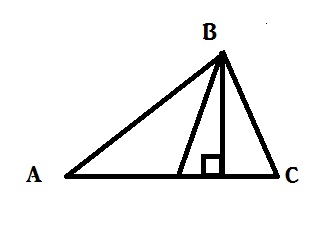
Два угла треугольника равны: С=63, А=27. Найти угол между высотой и медианой, проведенными из вершины третьего угла.

Answer 1

Для начала отыщу <B.
<B = 180 - (63 + 27) = 90. Это означает, что треугольник ABC прямоугольный.
В прямоугольном треугольнике медиана, проведённая из вершины прямого угла к гипотенузе, равна половине этой гипотенузе. Пусть медиана BM. Тогда треугольник  ABM - равнобедренный. Углы при его основании равны. <ABM = <A = 27 градусам.Далее найду <HMC, где H - основание высоты к AC.
Треугольник HBC также прямоугольный, <HBC = 90 - 63 = 27 градусов.
Тогда искомый угол равен 90 - 27 - 27 = 36 градусам. Это ответ.