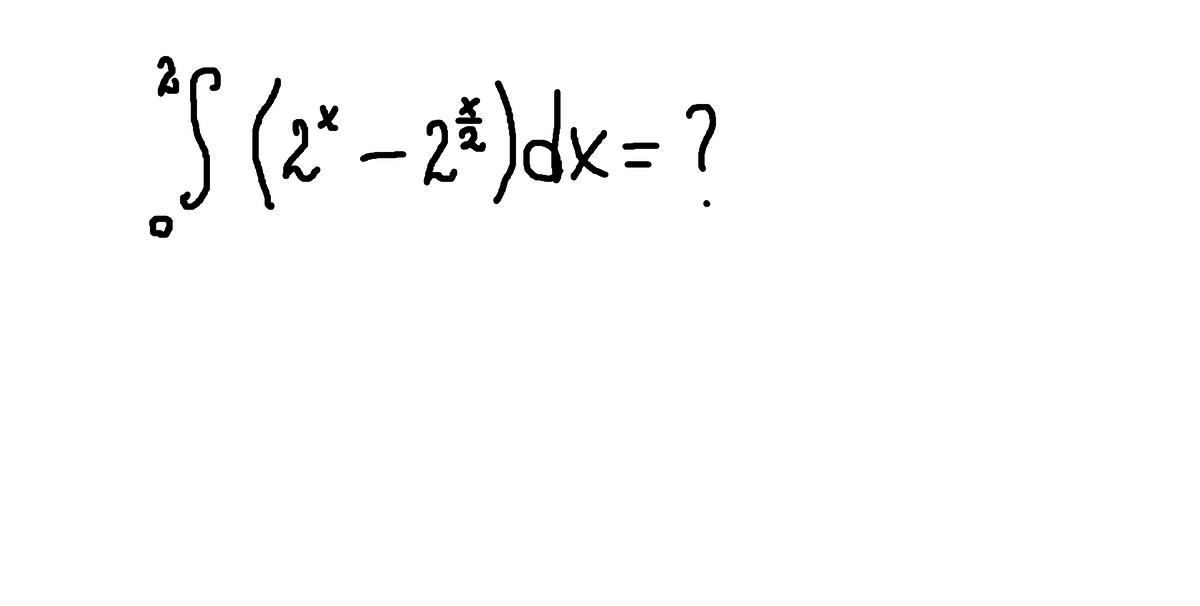Ответы
Ответ дал:
0
Ответ дал:
0
d(x/2)=(x/2)'dx=1/2dx
Ответ дал:
0
а все,спасибоЮ,поняла
Ответ дал:
0
спасибо вам ОГРОМНОЕ,разобралась.Сидела над ним наверно часа3
Ответ дал:
0
)))))
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад