Question

высота конуса равна 72 а длина образующей 78 найти площадь осевого сечения этого конуса

Answer 1

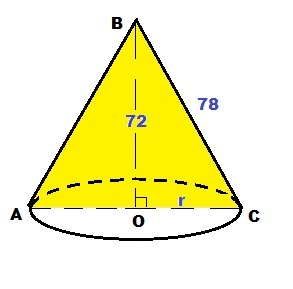
Осевое сечение конуса - равнобедренный треугольник ΔABC, основанием которого является диаметр основания конуса АС, а высотой - высота конуса ВО.

ΔВОС - прямоугольный : ∠ВОС = 90°.
Теорема Пифагора
ОС² = BC²-BO² = 78²-72² = (78-72)(78+72) = 6*150 = 900
OC = √900 = 30
AC = 2 OC  = 60
$S_{ABC}=frac{1}{2} *AC*BO = frac{1}{2} *60*72=2160$

Ответ: площадь осевого сечения конуса равна 2160 ед²