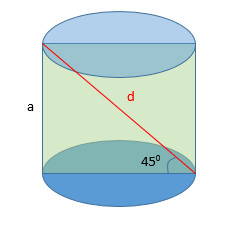
Диагональ осевого сечения цилиндра равна 10 см.и наклонена к плоскости основания под углом 45 градусов. вычислить площадь боковой поверхности цилиндра.
Ответы
Ответ дал:
0
В сечении получается прямоугольник. Если угол равен 45°, то это квадрат со стороной а
По т.Пифагора
2а²=d²
a=d/√2
Радиус окружности основания равен половине стороны квадрата
R=a/2=d/(2√2)
Площадь боковой поверхности равна произведению длины окружности на образующую
S=2πR*a=2πd/(2√2)*d/√2=2πd²/4=πd²/2
S=π*10/2=5π (см²)
Ответ: 5π≈15,7 см²
По т.Пифагора
2а²=d²
a=d/√2
Радиус окружности основания равен половине стороны квадрата
R=a/2=d/(2√2)
Площадь боковой поверхности равна произведению длины окружности на образующую
S=2πR*a=2πd/(2√2)*d/√2=2πd²/4=πd²/2
S=π*10/2=5π (см²)
Ответ: 5π≈15,7 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад