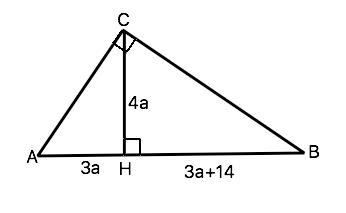
Катеты треугольника относятся как 3:4, а высота делит гипотенузу на отрезки, разница между которыми 14 см. Найти площадь
Ответы
Пусть в прямоугольном треугольнике АВС угол С=90°, АС:ВС=3:4 по условию. Высота прямоугольного треугольника делит гипотенузу на треугольники, подобные исходному и друг другу. Поэтому в ∆ АСН отношение АН:СН=3:4. Примем коэффициент этого отношения равным а. Тогда АН=3а, СН=4а, ВН=3а+14.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое проекций катетов на гипотенузу. СН²=АН•ВН => 16а²=3а•(3а+14) ⇒ 16а²-9а²=42а. При сокращении обеих сторон уравнения на а получим 7а=42, откуда а=6 см. Тогда высота СН=4•6=24 см, АВ=АН+ВН=6а+14=50 см. Площадь треугольника равна половине произведения высоты на длину стороны, к которой высота проведена.
S =CH•АВ/2=24•50:2=600 см²
============
Тот же результат получим, применив для решения отношение СН:ВН=3:4.