Question

Угол между высотами параллелограмма,
проведенными из вершины острого угла, в 4 раза больше этого угла. Найдите тупой
угол параллелограмма. 
ответ: 144 градус
дайте решение

Answer 1

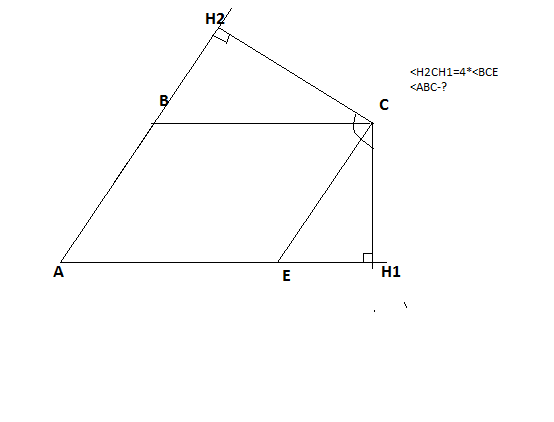
Построив высоты, получаем четырехугольник АН2СН1. Зная сумму углов четырехугольника, запишем:
<ВAЕ+<АH2С+<H2CH1+<СH1А=360
<ВAЕ=<BCE как противоположные углы параллелограмма. Углы СН1А и АH2С - прямые. <H2CH1=4*<BCE по условию. Подставим и перепишем: 
<BCE+90+4*<BCE+90=360
5*<BCE+180=360
5*<BCE=180
<BCE=36°
Острые углы параллелограмма по 36°. 
<АBС=<АEС=(360-2*36):2=144°