Ответы
Ответ дал:
0
Площадь равна площади криволинейной трапеции, ограниченной на участке [0;1]

В случае, когда получается отрицательное значение, надо брать его абсолютную величину.
S=13/3 (ед²)
В случае, когда получается отрицательное значение, надо брать его абсолютную величину.
S=13/3 (ед²)
Ответ дал:
0
Да.... поправил уже, спасибо
Ответ дал:
0
Решал через вышку, надеюсь, все верно.
Приложения:
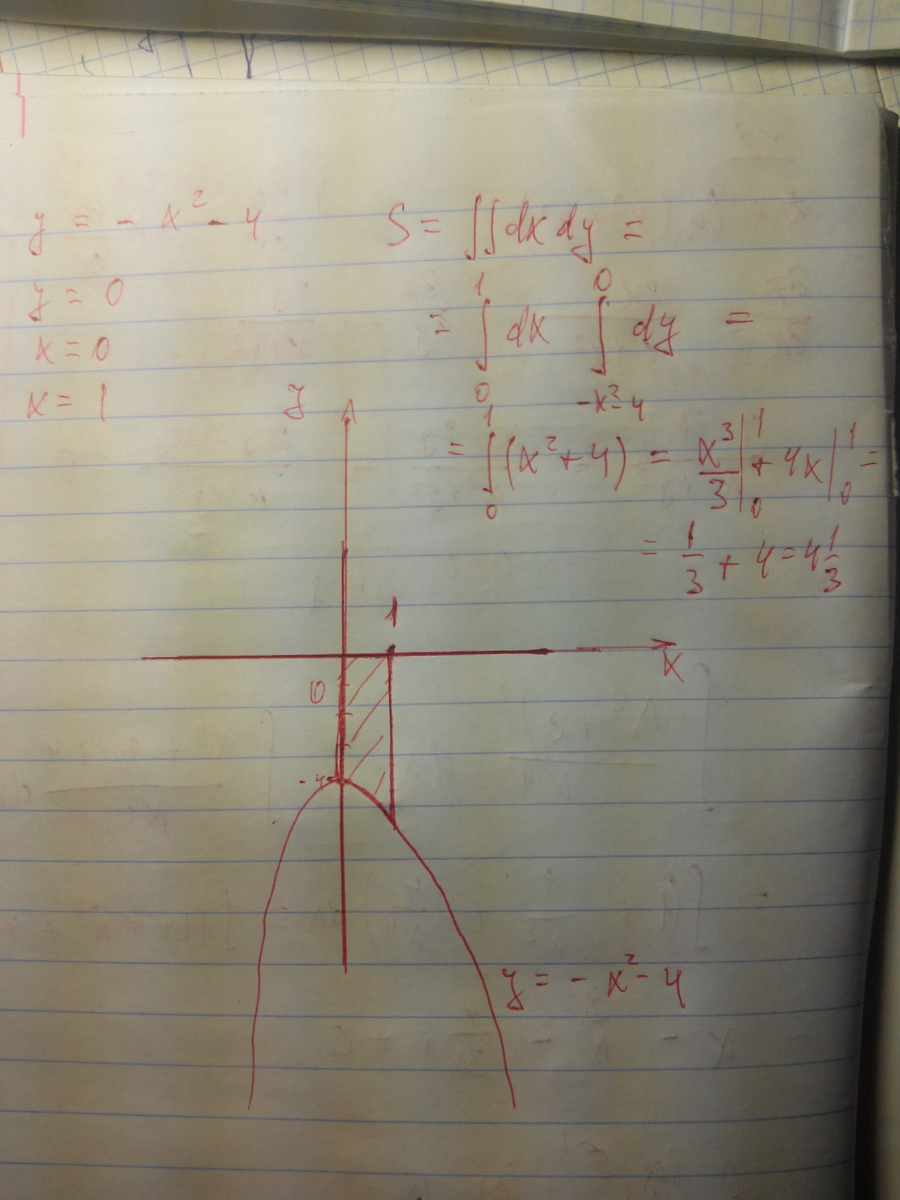
Ответ дал:
0
и даже с графиком! спасибо большое!!)
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад