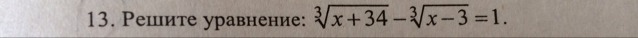Ответы
Ответ дал:
0
Решение:
Сделаем замену:

Тогда, уравнение примет вид:
![sqrt[3]{t+37} - sqrt[3]{t} = 1 sqrt[3]{t+37} - sqrt[3]{t} = 1](https://tex.z-dn.net/?f=sqrt%5B3%5D%7Bt%2B37%7D+-+sqrt%5B3%5D%7Bt%7D+%3D+1)
Выражение![sqrt[3]{t} sqrt[3]{t}](https://tex.z-dn.net/?f=sqrt%5B3%5D%7Bt%7D) переносим в правую часть, а 1 - в левую.
переносим в правую часть, а 1 - в левую.
Получится:
![sqrt[3]{t+37} - 1 = sqrt[3]{t} sqrt[3]{t+37} - 1 = sqrt[3]{t}](https://tex.z-dn.net/?f=sqrt%5B3%5D%7Bt%2B37%7D+-+1+%3D+sqrt%5B3%5D%7Bt%7D)
Возводим в куб все выражение:
![t+37-3(sqrt[3]{t+37})^2+3sqrt[3]{t+37}-1 = t \
36-3(sqrt[3]{t+37})^2+3sqrt[3]{t+37} = 0 t+37-3(sqrt[3]{t+37})^2+3sqrt[3]{t+37}-1 = t \
36-3(sqrt[3]{t+37})^2+3sqrt[3]{t+37} = 0](https://tex.z-dn.net/?f=t%2B37-3%28sqrt%5B3%5D%7Bt%2B37%7D%29%5E2%2B3sqrt%5B3%5D%7Bt%2B37%7D-1+%3D+t+%5C%0A36-3%28sqrt%5B3%5D%7Bt%2B37%7D%29%5E2%2B3sqrt%5B3%5D%7Bt%2B37%7D+%3D+0)
Сделаем еще одну замену:
![z=sqrt[3]{t+37} z=sqrt[3]{t+37}](https://tex.z-dn.net/?f=z%3Dsqrt%5B3%5D%7Bt%2B37%7D)
Теперь уравнение стало квадратным:

Относительно второй замены решаем следующие уравнения:
![sqrt[3]{t+37} = 4 \
t+37 = 64 \
t_1 = 27 \
sqrt[3]{t+37} = -3 \
t+37 = -27 \
t_2 = -64 sqrt[3]{t+37} = 4 \
t+37 = 64 \
t_1 = 27 \
sqrt[3]{t+37} = -3 \
t+37 = -27 \
t_2 = -64](https://tex.z-dn.net/?f=sqrt%5B3%5D%7Bt%2B37%7D+%3D+4+%5C%0At%2B37+%3D+64+%5C%0At_1+%3D+27+%5C%0Asqrt%5B3%5D%7Bt%2B37%7D+%3D+-3+%5C%0At%2B37+%3D+-27+%5C%0At_2+%3D+-64)
Зная, что t=x-3, опять же решаем уравнения:

Итого:
Ответ:
Сделаем замену:
Тогда, уравнение примет вид:
Выражение
Получится:
Возводим в куб все выражение:
Сделаем еще одну замену:
Теперь уравнение стало квадратным:
Относительно второй замены решаем следующие уравнения:
Зная, что t=x-3, опять же решаем уравнения:
Итого:
Ответ:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад