Question

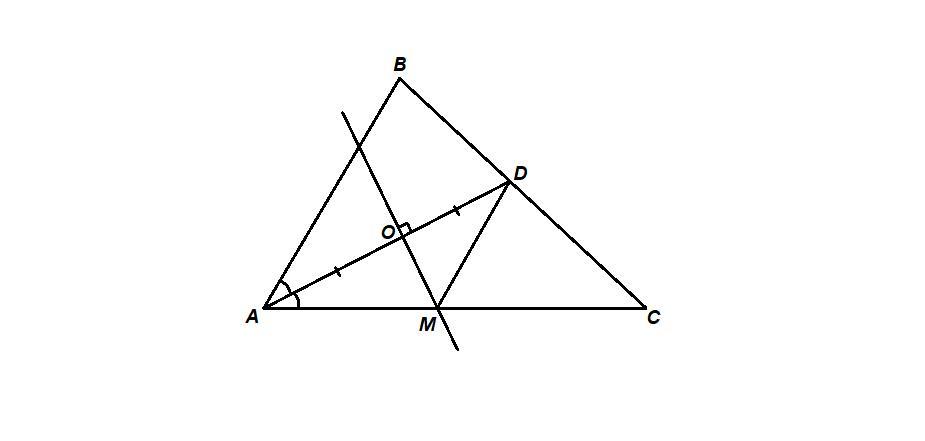
Прямая, проходящая через середину биссектрисы AD треугольника ABC и перпендикулярная к AD, пересекает сторону AC в точке М. Докажите, что MD||AB

Answer 1

Ответ:

МО - серединный перпендикуляр к отрезку AD, а все точки серединного перпендикуляра к отрезку равноудалены от концов отрезка, значит

МА = MD.

Следовательно, треугольник AMD равнобедренный, тогда его углы при основании равны:

∠MDA = ∠MAD,

но ∠MAD = ∠BAD, так как AD - биссектриса угла А, значит

∠MDA = ∠BAD, а эти углы - внутренние накрест лежащие при пересечении прямых MD и АВ секущей AD, значит

MD ║ AB.