Ответы
Ответ дал:
0
Всё подробно написала в решении.Во 2) допиши,что это скалярное произведение векторов.
Приложения:
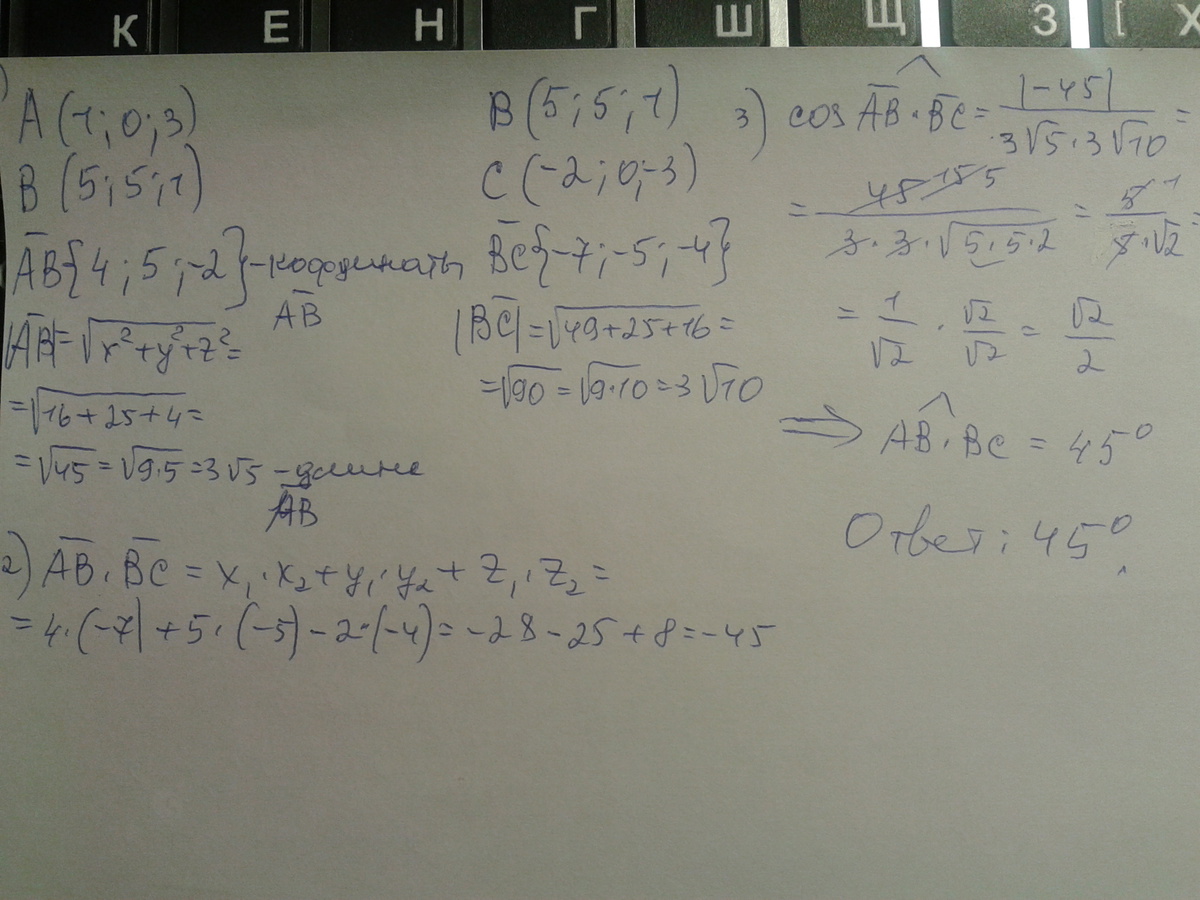
Ответ дал:
0
Сначала найдем координаты каждого вектора:


Теперь найдем модуль каждого вектора:


Ищем скалярное произведение через координаты:

скалярное произведение через модули и косинус угла:


Поскольку косинус отрицательный, то угол равен 135.
Ответ:
Теперь найдем модуль каждого вектора:
Ищем скалярное произведение через координаты:
скалярное произведение через модули и косинус угла:
Поскольку косинус отрицательный, то угол равен 135.
Ответ:
Приложения:
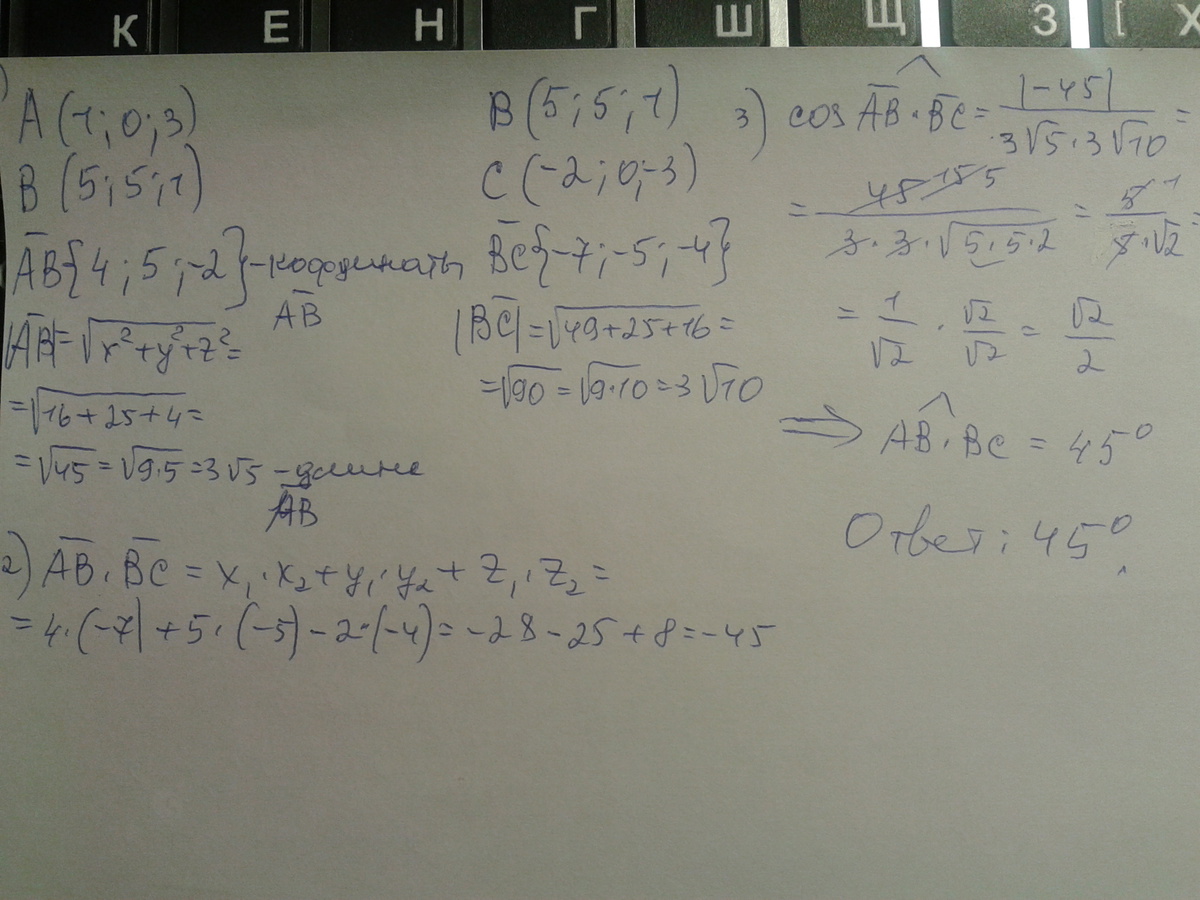
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад