Question

Люди сидим спорим с мамой на счёт этой задачи рассудите нас)В треугольнике ABC медианы пересекаются в точке М. Известно, что угол MAB=угол MBA, угол MCB=угол MBC. Найдите угол ABC.

Answer 1

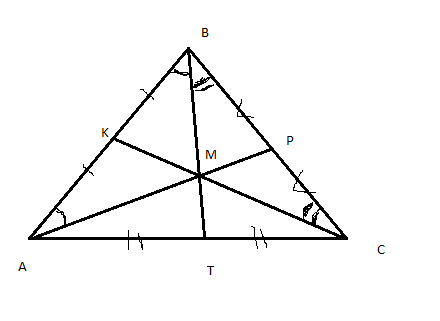
См. рисунок.
Треугольник МАВ-равнобедренный, значит АМ=ВМ
Треугольник МВС- равнобедренный, значит ВМ=СМ.
В итоге АМ=ВМ=СМ
Так как медианы в точке пересечения делятся в отношении2:1 считая от вершины,
поэтому все медианы равны между собой.
Более того из треугольника МАВ следует, что МК перпендикулярна АВ, значит и СК перпендикуляр к АВ, т.е медиана СК является и высотой. И биссектрисой,что следует из равенства треугольников АСК и СКВ: уголМСВ=углу МСА и по условию ещё и углу МВС
Аналогично, МР- перпендикуляр к ВС, АР- медиана и высота. И биссектриса, что следует из равенства треугольников АРС и АРВ.
Угол ВАМ=углу САМ и равен углу МВА по условию
Треугольники АМТ и ТМС равны по трем сторонам и угол ТАМ=углу ТСМ.
Все углы треугольника равны.
Треугольник равносторонний. Угол АВС=60⁰
 

Answer 2

Спасибо огромное)