Question

Тангенс угла С треугольника АВС равен 3/4, D - отличная от А точка пересечения окружностей , построенных на сторонах АВ и АС как на диаметрах . Известно что  DВ:DС=9:16 .Найти угол А . Желательно с рисунком и как можно подробнее 

Answer 1

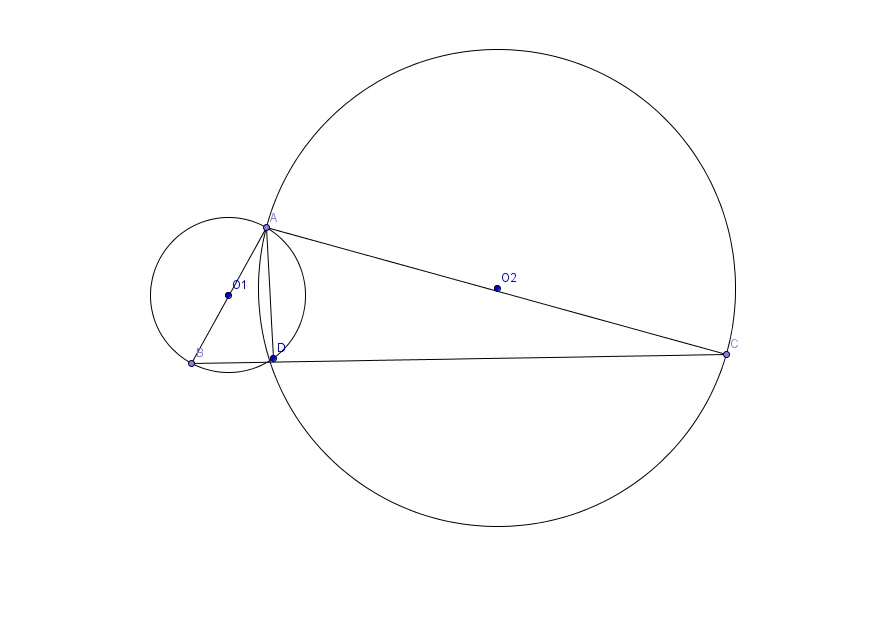
Что дано и обозначения писать не буду, все на рисунке.
∟ADB=∟ADC=90° (так как это вписанные в окружность углы, которые опираются на диаметры), пусть х- коэффициент пропорциональности, тогда BD=9x, CD=16x, из прямоугольного треугольника ADC, AD=DC*tgC=16x*3/4=12x, по т. Пифагора найдем АВ и АС, АВ=15х,  АС=20х. Заметим, что (15х)^2+(20х)^2=(25х)^2, то есть, АВ^2+АС^2=ВС^2, следовательно по теореме обратной теореме Пифагора угол А=90 градусов.