Question

Задача средней сложности на нахождение площади треугольника. Эта задачка была сегодня на вступительных экзаменах МГТУ им. Баумана (так, чтоб вы знали чем имеете дело) и классифицировалась как легкая. Я ее решить не смог, прошу помощи у вас. 

Answer 1

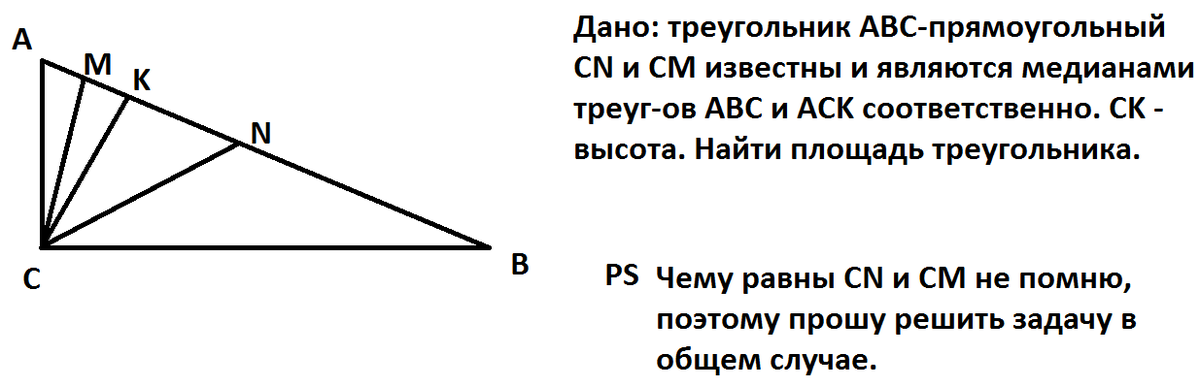
Буду считать, что длины адекватные и треугольник из условия существует (определять "в общем случае" ограничения на CN и CM я не хочу).

Медиана, проведенная к гипотенузе, равна половине последней (для док-ва достаточно удвоить медиану и заметить, что получился прямоугольник), так что AB = 2CN = c

Проведем медиану BX, из подобия треугольников AKC и ABC следует, что CM : BX = AC : AB или AC * BX = CM * AB = 2CM * CN = x

Теперь имеем такую задачу: найти площадь прямоугольного треугольника с гипотенузой c, если произведение длин медианы и катета, к которому проведена медиана, равно x.

Её уже можно решать как угодно. Например, так:
Пусть катеты a и b, медиана ma = x/a. Теорема Пифагора для маленького и большого треугольников:
b^2 = ma^2 - (a/2)^2 = с^2 - a^2 - имеем уравнение на a^2.
4x^2 / a^2 - a^2 = 4c^2 - 4a^2
3a^4 - 4c^2 a^2 + 4x^2 = 0 - квадратное уравнение, пусть имеет 2 корня:
a^2 = (2c^2 +- sqrt(4c^4 - 12x^2)) / 3 = c^2 / 3 + (c^2 +- sqrt(4c^4 - 12x^2)) / 3
Оба корня положительны, так что всё в порядке.
b^2 = c^2 - a^2 = (c^2 -+ sqrt(4c^4 - 12x^2)) / 3 = 
4S^2 = a^2 b^2 = c^2 (c^2 -+ sqrt(4c^4 - 12x^2)) / 9 + (12x^2 - 3c^4) / 9
4S^2 = (12x^2 - 2c^4 -+ sqrt(4c^4 - 12x^2))/9
S^2 = 4/9 * (12x^2 - 2c^4 -+ sqrt(4c^4 - 12x^2))
S = 2/3 * sqrt(12x^2 - 2c^4 -+ sqrt(4c^4 - 12x^2))

Можно возвратиться и к исходным переменным, но намного красивей не станет.

2 решения возникают из-за того, что высота делит прямоугольник на 2 треугольника, и высота может быть проведена в каждом из них. Соответственно, возникают две конфигурации.
Вероятно, что одно решение будет в случае равнобедренного треугольника.

Answer 2

 Обозначим катеты $a,b$  ,тогда гипотенуза  $c=sqrt{a^2+b^2}$ 
 $CN=AN=NB = frac{c}{2}\\ CN=frac{sqrt{a^2+b^2}}{2}$ 
 Высота $CK=frac{ab}{sqrt{a^2+b^2}}$ 
  Положим что $S_{ABC}=frac{ab}{2}=S\ ab=2S$ 
с выражения $CN=frac{sqrt{a^2+b^2}}{2}\ sqrt{a^2+b^2}=2CN$ 
   Из треугольников $AMK;MKC$  по теореме косинусов и теореме Пифагора соответственно получаем 
 $AM=MK\ CM^2=AM^2+frac{a^2b^2}{a^2+b^2}\ CM^2=AM^2+b^2-2AM*b*frac{b}{sqrt{a^2+b^2}}\\ frac{S^2}{CN^2} = b^2-AM*frac{b^2}{CN}\\ frac{S^2}{CN^2} = b^2(1- frac{AM}{CN}) \\ AM=MK=sqrt{CM^2-frac{S^2}{ CN^2 }}=AM\\ frac{S^2}{CN^2} =b^2(1-frac{ sqrt{CM^2-frac{S^2}{CN^2}}}{CN})$
 $AN=NC\ b^2=2CN^2-2CN^2 * cosKNC\ CN=frac{frac{ab}{sqrt{a^2+b^2}}}{sinKNC}\ sinKNC = frac{S}{CN^2}\\ cosKNC=sqrt{frac{CN^4-S^2}{CN^4}}\ b^2=2CN^2(1-sqrt{frac{CN^4-S^2}{CN^4}})$

$frac{S^2}{CN^2} =b^2(1-frac{ sqrt{CM^2-frac{S^2}{CN^2}}}{CN})\ frac{S^2}{CN^2}=(2CN^2(1-sqrt{frac{CN^4-S^2}{CN^4}}))*(1-frac{ sqrt{CM^2-frac{S^2}{CN^2}}}{CN})$ 

 
 
 
 
Откуда 
$S=frac{2}{3}sqrt{-2*CN^2+3*CN^2*CM^2-sqrt{CN^6(4*CN^2-3CM^2)}$