Question

Есть два круга
с радиусами 16 и 9, которые прикасаются внешним образом. Построенная трапеция так, что
каждый круг прикасается к двум боковым сторонам и
одной из основ. Какое минимальное значение может принимать длина боковой стороны ?

Answer 1

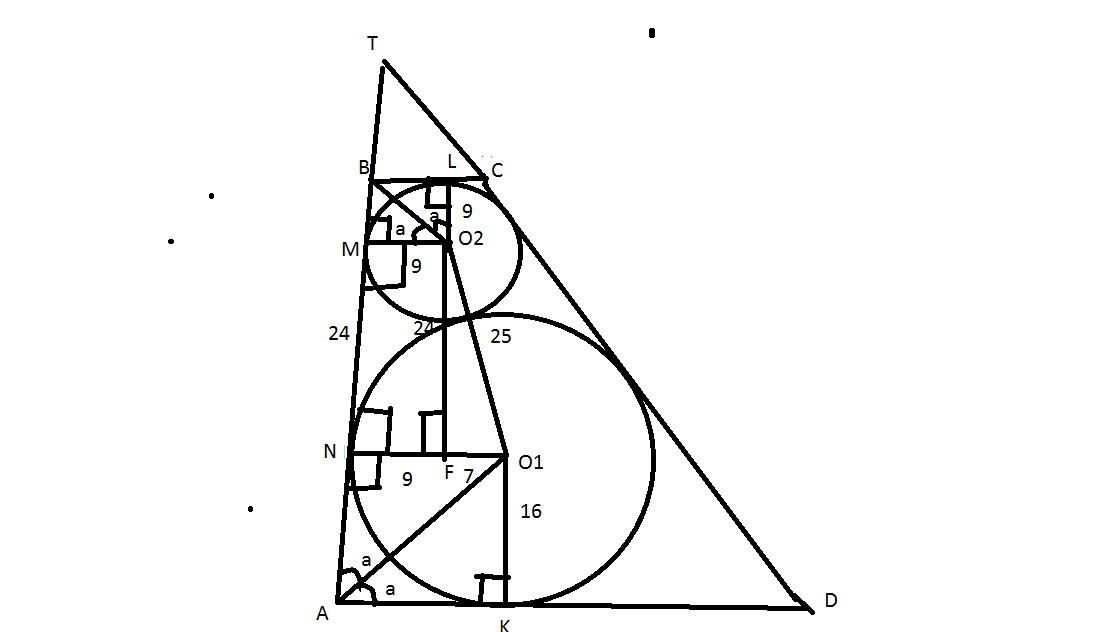
Из рассуждений  представленных на рисунке  и сделанных построений видно  что:
NM=sqrt(25^2-7^2)=24
Продлив стороны трапеции  до пересечения в точке T,то угол A=B ,как  соответственные,откуда  угол MBL=180-A  как   смежный угол.
Прямоугольные треугольники  MO2B и  BO2L  равны по общей гипотенузе  и катетам  равными как   радиусы окружности,по той же причине  равны треугольники  NAO1 и AKO1
Откуда угол  NAO1=KAO1=a,  угол O2BM=O2BL=(180-A)/2= (180-2a)/2=90-a
Откуда угол  BO2M=NAO1=a
Для того  чтобы   наглядно показать ,что  решение охватывает все случаи возможных трапеций,возьмем  в качестве параметра угол a (что  вдвое меньше угла   основания)
Тогда боковая сторона   будет представляться выражением:S=16/tga+9*tga+24,выделяя полный  квадрат получим: S=(4/√tga -3√tga)^2+48 ,тк   квадрат  не  отрицателен,то  очевидно  наименьшее  значение  когда: 4/√tga-3*√tga=0  ,то Smin=48
Ответ:48
Теперь я немного дополню свое  решение  найдя  ради  интереса  сам угол a!!!
4/√tga-3√tga=0
заменим: √tga =t  >0  tga>0  что  верно  тк это угол  острый.
4/t-3t=0
4-3t^2=0
t^2=4/3
То  есть
tga=4/3
То есть  угол не  так хорош как  нам казалось.
Если для интереса  посмотреть каков же примерно это угол,то  получим:53  градуса  с копейками. А  сам угол  основания  около 106 градусов,а  значит  наша трапеция нестандартного  вида.

Answer 2

Тут есть 2 парадокса (кто знает, что такое "парадокс"?). 1) аналоговое мышление - следствие воображения, а воображение не признает "законов природы". 2) в математике (и вообще в "точных" науках, обратите внимание на кавычки) воображение и интуиция должны оперировать именно с "цифровым материалом". То есть "играть на поле противника".

Answer 3

Но учить концентрации - это отдельный вид ПЕДАГОГИКИ. То есть это еще надо уметь делать так, чтобы не убить воображение и не убить мотивацию, а наоборот - развить её. На мой взгляд, этого можно достичь через постоянные соревнования и - одновременно - постоянное сотрудничество. Есть аналог такого обучения - в шахматных школах высокого уровня.

Answer 4

Вот меня например было совершенно бессмысленно учить теоремам. Я ПОНИМАЛ геометрию (и до сих пор понимаю) интуитивно. Я сочиняю теоремы, которые не знаю, и нахожу связи, которые ДОЛЖНЫ БЫТЬ, просто потому, что они ДОЛЖНЫ БЫТЬ. Так было со школы. Но развил я свои способности и знания до какого-то приличного (более-менее) уровня только вот недавно, когда откровенно говоря, было уже поздно. Просто сам захотел от скуки.