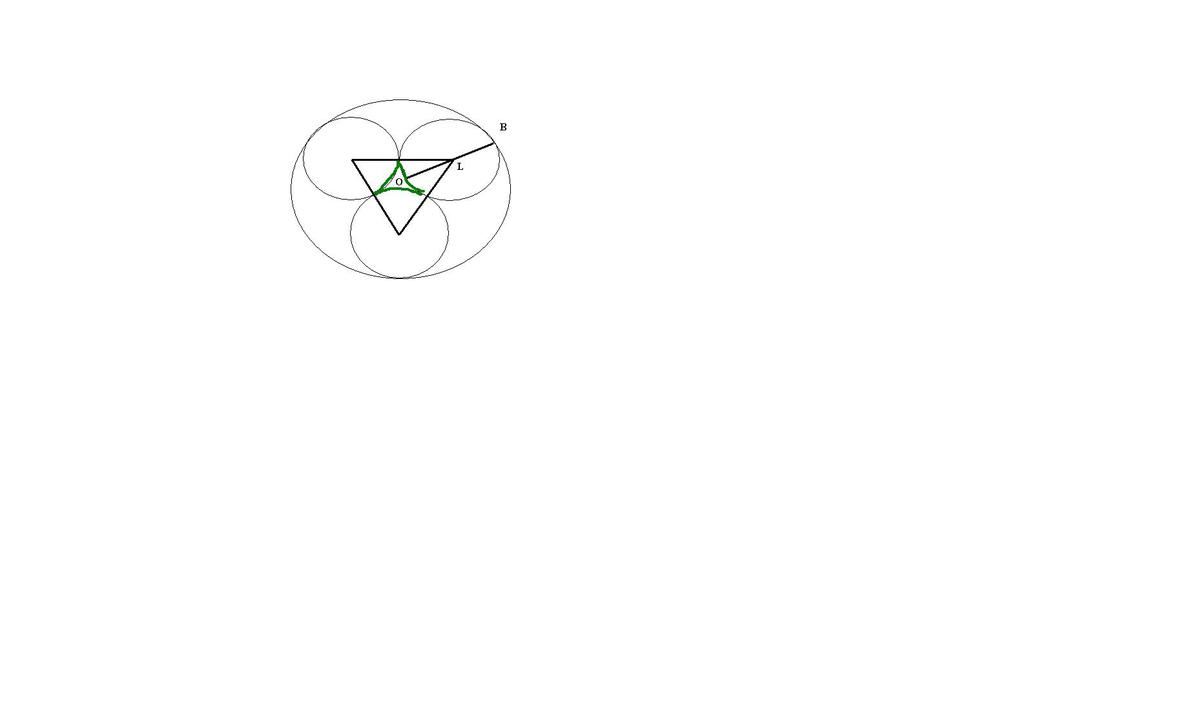
В окружность, радиус которого равен 2+корень из 3, вписаны три равных окружностей, которые соприкасаются. Найти площадь фигуры, которая образуется при соприкосновении этих окружностей (маленький треугольник в центре )?
Ответы
Ответ дал:
0
Соединим три окружности , получим правильный треугольник , т ак как три окружности расположены симметрично друга от друга

В сумме радиус описанной около треугольника окружности с
радиус описанной около треугольника окружности с 

Площадь треугольника

Площадь сектора

Площадь треугольника

В сумме
Площадь треугольника
Площадь сектора
Площадь треугольника
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад