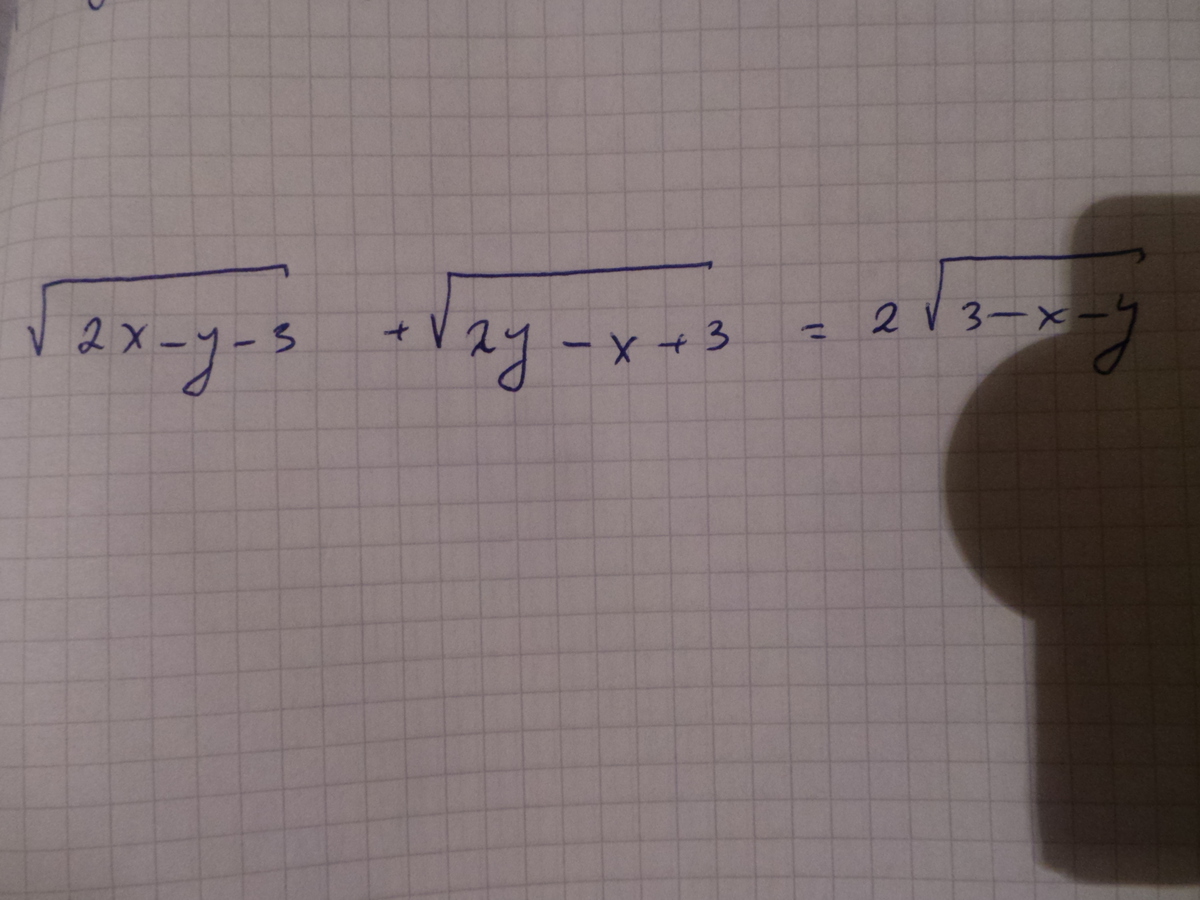Ответы
Ответ дал:
0
решения описывают треугольник с вершинами координаты
и целые решения будут
так же нужно рассмотреть 3 варианта , но они не подходят
Есть решение в рациональных числах
Ответ дал:
0
2x-y-3>=0 2x-y>=3
2y-x+3>=0
3-x-y>=0
Сложим 1 и 2 неравенство
x+y>=0
из 3
x+y<=3
То есть возможно 4 варианта:
1) x+y=1
y=1-x
sqrt(3x-4)+sqrt(5-3x)=2sqrt(2)
sqrt
3x-4>=0 x>=4/3 x<=5/3
5-3x>=0
целых решений нет.
2)x+y=2
y=2-x
sqrt(3x-5)+sqrt(7-3x)=2
3x-5>=0 x>=5/3
7-3x>=0 x<=7/3
На этом промежутке есть единственное возможное целое решение x=2
Проверим: sqrt(1)+sqrt(1)=2
x=2 y=0
3)x+y=3 y=3-x
sqrt(3x-6)+sqrt(9-3x)=0 (тк корни не отрицательны)
3x-6=0 нет решений
9-3x=0
4) И наконец последний случай:
x+y=0 x=-y
sqrt(3x-3)+sqrt(3-3x)=2*sqrt(3)
3x-3>=0
3-3x>=0
ТО есть только если
3-3x=0
x=1
0+0=2*sqrt(3) невозможно
Ответ :x=2 y=0
2y-x+3>=0
3-x-y>=0
Сложим 1 и 2 неравенство
x+y>=0
из 3
x+y<=3
То есть возможно 4 варианта:
1) x+y=1
y=1-x
sqrt(3x-4)+sqrt(5-3x)=2sqrt(2)
sqrt
3x-4>=0 x>=4/3 x<=5/3
5-3x>=0
целых решений нет.
2)x+y=2
y=2-x
sqrt(3x-5)+sqrt(7-3x)=2
3x-5>=0 x>=5/3
7-3x>=0 x<=7/3
На этом промежутке есть единственное возможное целое решение x=2
Проверим: sqrt(1)+sqrt(1)=2
x=2 y=0
3)x+y=3 y=3-x
sqrt(3x-6)+sqrt(9-3x)=0 (тк корни не отрицательны)
3x-6=0 нет решений
9-3x=0
4) И наконец последний случай:
x+y=0 x=-y
sqrt(3x-3)+sqrt(3-3x)=2*sqrt(3)
3x-3>=0
3-3x>=0
ТО есть только если
3-3x=0
x=1
0+0=2*sqrt(3) невозможно
Ответ :x=2 y=0
Ответ дал:
0
Я зачем свое драгоценное время тогда терял написал бы ответ и все
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад