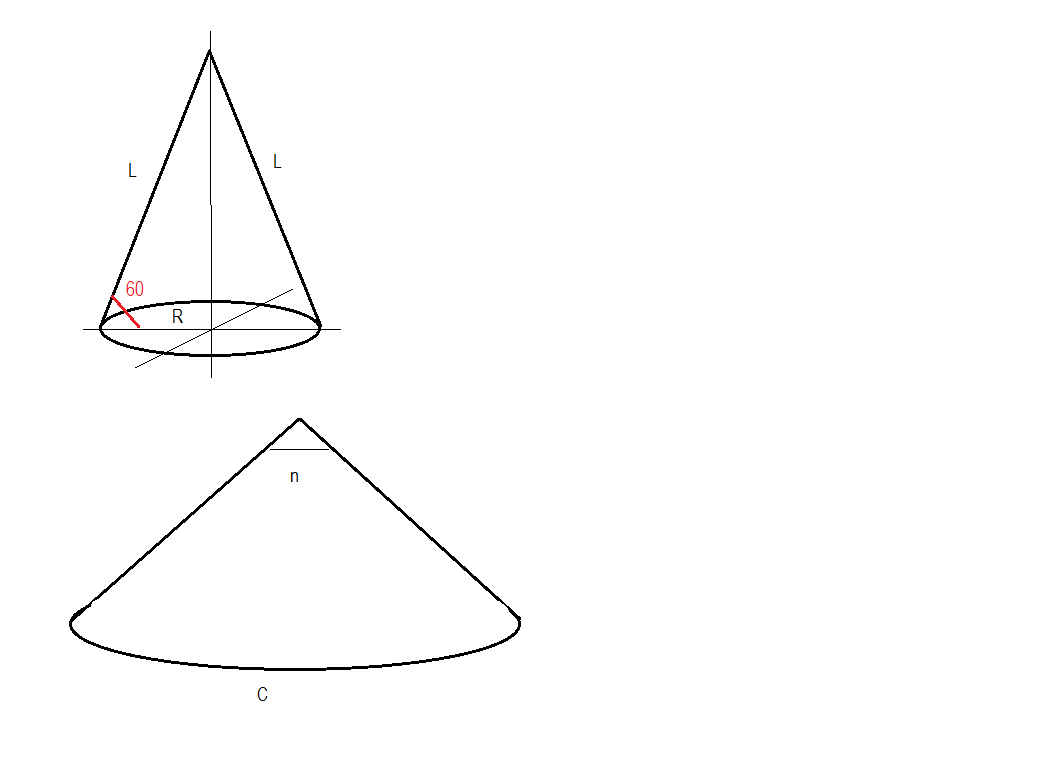
Помогите пожалуйста решить. Образующая конуса равна 40 см и наклонена к плоскости основания под углом 60 градусов. найдите площадь боковой поверхности конуса. Напишите с подробным объяснением. Заранее спасибо
Ответы
из вершины конуса надо опустить перпендикуляр на основание. пусть это будет AH.точка H как раз будет находиться на диаметре окружности(основания).пусть диаметр будет MN. следовательно,мы получим прямоугольный треугольник AHN,в котором угол ANH=60 градусов. r=HN=cos60*40=20(т.к. HN-прилежащий катет,а AN- гипотенуза ---> cos60=HN/AN,где AN-образующая).
S=Pi*r*l=Pi*AN*HN=3.14*20*40=2512
Образующая конуса равна 40 см и наклонена к плоскости основания под углом 60 градусов
L=40 см
<a= 60
радиус основания R= L*cos60
длина окружности основания С=2pi*R=2pi*cos60
боковая поверхность конуса - это сектор окружности с радиусом L и длиной дуги С
найдем центральный угол сектора n=2C/L=2*2pi*cos60/L =4pi*cos60/L
площадь сектора считаем по формуле
S =1/2*L^2*n =1/2*L^2*4pi*cos60/L=L*2pi*cos60= 40*2pi*cos60= 40pi
Ответ 40pi или 40п