Question

Очень нужна помощь! Заранее спасибо.Кто ответит, тому 112 баллов.
Внутри треугольника ABC взята точка M, через которую проведены прямые, параллельные всем его сторонам. Площади трех образовавшихся треугольников с общей вершиной M равны S1, S2, S3. Найдите площадь треугольника ABC.

Answer 1

назовем треугольники W1, W2, W3.
а параллелограммы на вертикальных углах I, II,  III соответственно.
пусть при вершине М - углы в W1 и I = альфа; W2 и II = бета; W3 и III = гамма

Пусть вершины треугольника W1 буду MEF, W2 MGH, W3 MPQ
Заметим, что треугольники W1, W2, W3 подобны, тк все три угла у них равны

Запишем площади W1, W2, W3, I,II,III
S1 = $frac{ME*MF*sin alpha }{2}$
S2 = $frac{MG*MH*sin beta }{2}$
S3 = $frac{MP*MQ*sin gamma }{2}$

I = $MP*MH*sin alpha$
II = $MQ*ME*sin beta$
III= $MF*MG*sin gamma$

Запишем отношения

I/S1 = $frac{2*MP*MH*sin alpha }{ME*MF*sin alpha } = frac{2*MP*MH}{ME*MF}$
Аналогично
II/S2 = $frac{2*MQ*ME}{MG*MH}$
III/S3 = $frac{2*MF*MG}{MP*MQ}$

то есть: I = S1* $frac{2*MP*MH}{ME*MF}$
II = S2*$frac{2MQ*ME}{MG*MH}$
III = S3*$frac{2MF*MG}{MP*MQ}$

S(ABC) = S1+S2+S3+I+II+III  обозначим это равенство (!)

Из подобия треугольников W1, W2, W3 получаем:

$frac{MH}{ME} = sqrt{ frac{S2}{S1} }$
$frac{MP}{MF} = sqrt{ frac{S3}{S1} }$

$frac{MQ}{MG} = sqrt{ frac{S3}{S2} }$
$frac{ME}{MH} = sqrt{ frac{S1}{S2} }$

$frac{MF}{MP} = sqrt{ frac{S1}{S3} }$
$frac{MG}{MQ} = sqrt{ frac{S2}{S3} }$

А теперь если подставить все это счастье в равенство (!), получим

S(ABC) = $S1+S2+S3 + 2* sqrt{S2*S3} +2* sqrt{S1*S3} +2* sqrt{S1*S2}$

то есть $S(ABC) = ( sqrt{S1} + sqrt{S2} + sqrt{S3} )^{2}$

Answer 2

реально красивая задача:) Respect

Answer 3

Благодаря параллельности прямых, все образовавшиеся треугольники подобны друг другу и исходному ΔАВС (по трём углам).
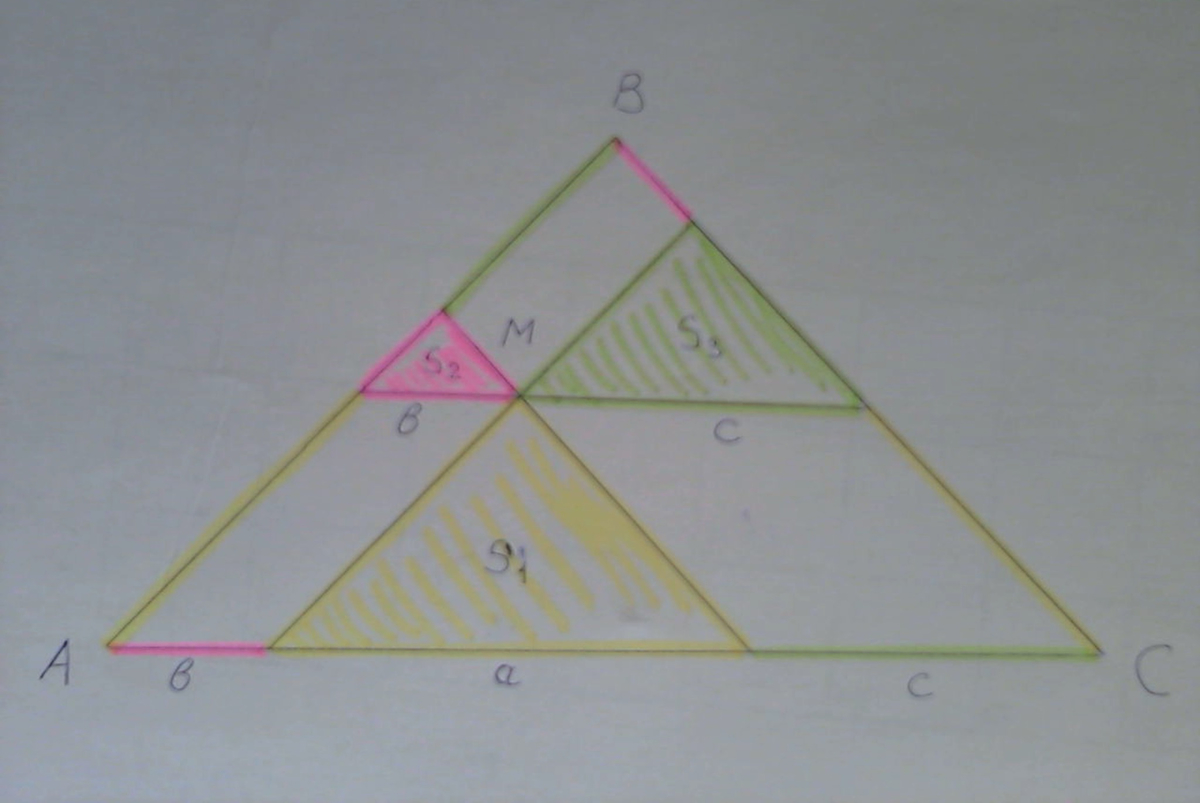
Обозначим стороны получившихся треугольников, параллельные стороне АС как a, b и с, их площади как S₁, S₂ и S₃ (см. рис. в прикреплённом файле).
Площадь S ΔАВС относится к площади S₁ подобного треугольника, как квадрат отношения соответствующих сторон:
$frac{S}{ S_{1}}$ = $(frac{b+a+c}{a})^{2}$ = $(1+frac{b}{a}+frac{c}{a})^{2}$       (1)
Отношение соответствующих сторон подобных треугольников равно корню квадратному из отношений их площадей:
$frac{b}{a}$ = $sqrt{ frac{S_{2}}{S_{1}}}$       (2)
$frac{c}{a}$ = $sqrt{ frac{S_{3}}{S_{1}}}$       (3)
Подставляем (2) и (3) в (1):
$frac{S}{ S_{1}}$ = $(1 +sqrt{ frac{S_{2}}{S_{1}}}+sqrt{ frac{S_{3}}{S_{1}}})^{2}$ = $frac{(sqrt{S_{1}}+sqrt{S_{2}}+sqrt{S_{3}})^{2}}{S_{1}}$
Откуда окончательно получаем:
S =  $(sqrt{S_{1}}+sqrt{S_{2}}+sqrt{S_{3}})^{2}}$