Question

Найдите площадь треугольника ABC, если две его медианы BH и AK взаимно перпендикулярны и равны соответственно 3 см и 2 см. Решите,пожалуйста

Answer 1

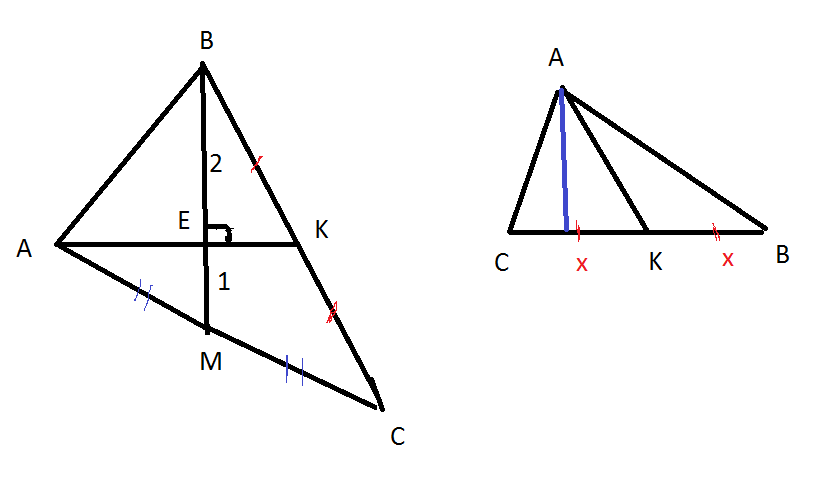
Медианы в точке пересечения делятся в отношении 2:1, считая  от вершины, поэтому
ВЕ=2, ЕМ=1
Площадь треугольника  АВК равна половине произведения основания АК=2 и высоты ВЕ=2
S=1/2·2·2=2
Треугольники АВК и АКС равновелики, у них одинаковые площади, так как одинаковые основания х и одинаковая высота ( синим цвето на рис.2)
Поэтому площадь треугольника
АКС тоже равна 2,
а площадь треугольника АВС равна сумме площадей треугольника АВК и АСК.
ОТвет.4