Question

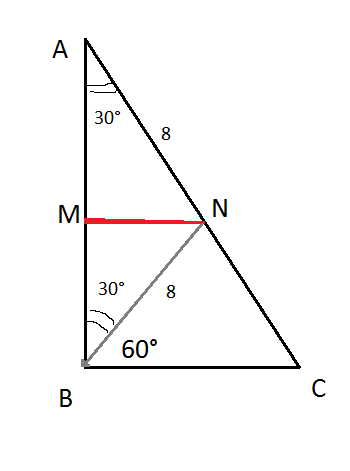
Через середину М катета прямоугольного треугольника АВС проведено прямую,КОТОРАЯ ПАРАЛЛЕЛЬНА КАТЕТУ И ПЕРЕСЕКАЕТ гипотенузу АС в точке N.Довести,что AN=NB.НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКА AMN,если BN=8 см,угол NBC=60 град.

Answer 1

МN || АС, значит MN ⊥ АВ
Прямоугольный треугольник АМN равен прямоугольному треугольнику BMN  по двум катетам:
МN - общая сторона
AM = MB  по условию ( М- середина АВ)
Из равенства треугольников следует, АN = BN=8 см
Так как угол NBC  равен 60°, то угол АВN равен  90°-60°=30°.
В прямоугольном треугольнике катет против угла в 30° равен половине гипотенузы.
MN= 4 см.
По теореме Пифагора из прямоугольного треугольника АMN:
АМ²=AN²-MN² = 8² - 4²=64 - 16 = 48
AM = 4√3 cм
S (Δ AMN) = (AM· MN)/2 = (4√3·4)/2=8√3 кв. см