Ответы
Ответ дал:
0
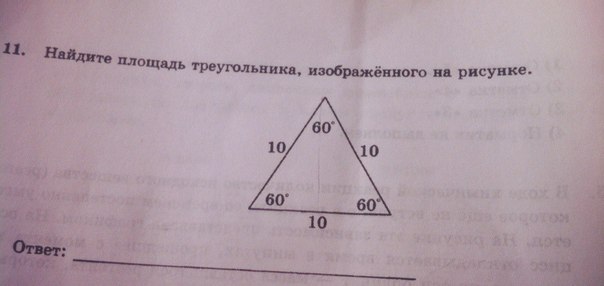
Дано: ABC - равносторонний треунольник: ∠A=∠B=∠C=60градусов. АВ=ВС=АС=10.
Найти:
Решение:
Так как с рисунка видно что ∠А=∠В=∠С=60градусов и АВ=ВС=АС=10, то имеем что треугольник равносторонний. АК = СК = АС/2=10/2 = 5.
С прямоугольного треугольника ABK (∠АКВ = 90градусов)
по т. Пифагора определим высоту ВК

Определим площадь равностороннего треугольника

Ответ:
Найти:
Решение:
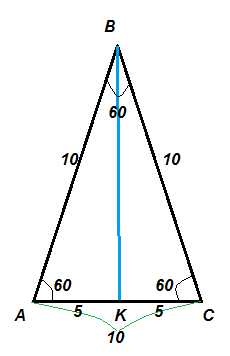
Так как с рисунка видно что ∠А=∠В=∠С=60градусов и АВ=ВС=АС=10, то имеем что треугольник равносторонний. АК = СК = АС/2=10/2 = 5.
С прямоугольного треугольника ABK (∠АКВ = 90градусов)
по т. Пифагора определим высоту ВК
Определим площадь равностороннего треугольника
Ответ:
Приложения:
Ответ дал:
0
Спасибо огромное)
Ответ дал:
0
На здоровье)
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад