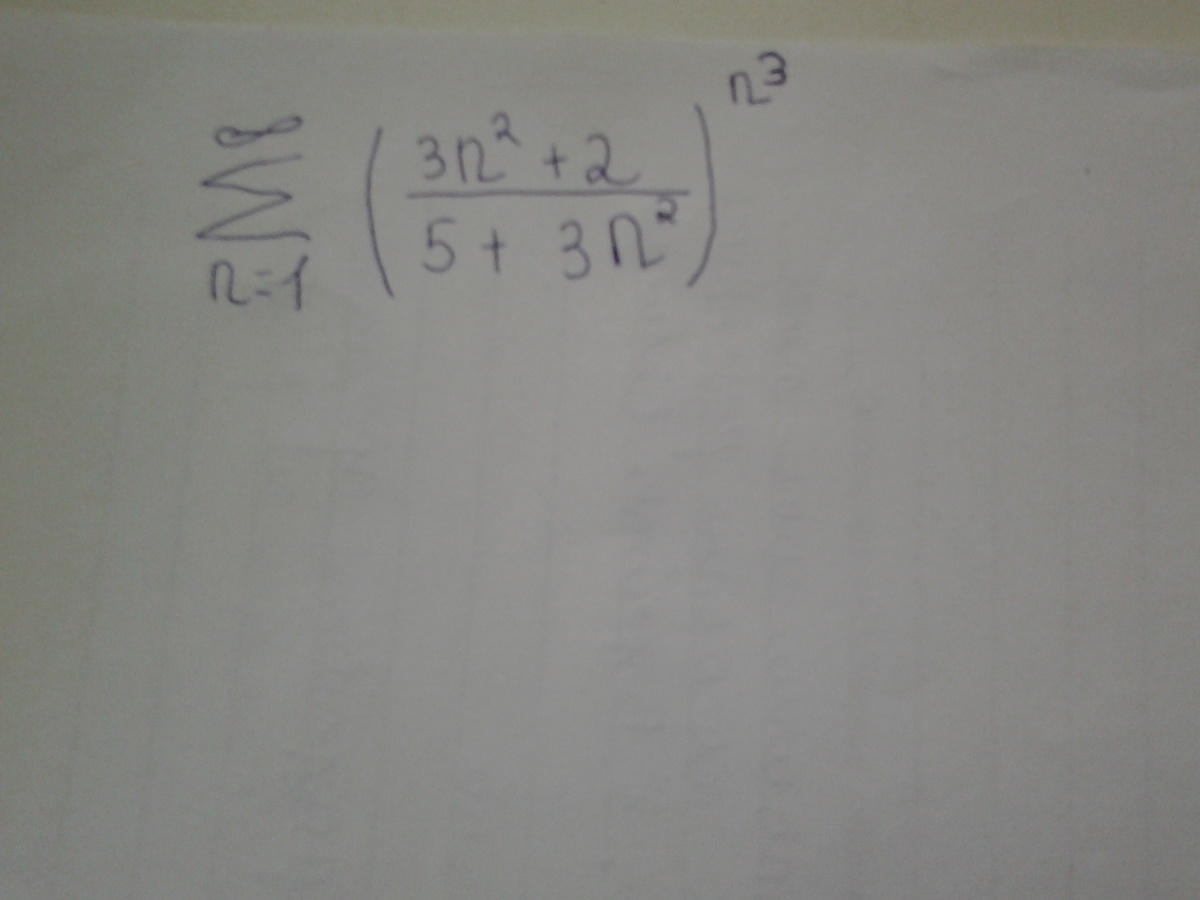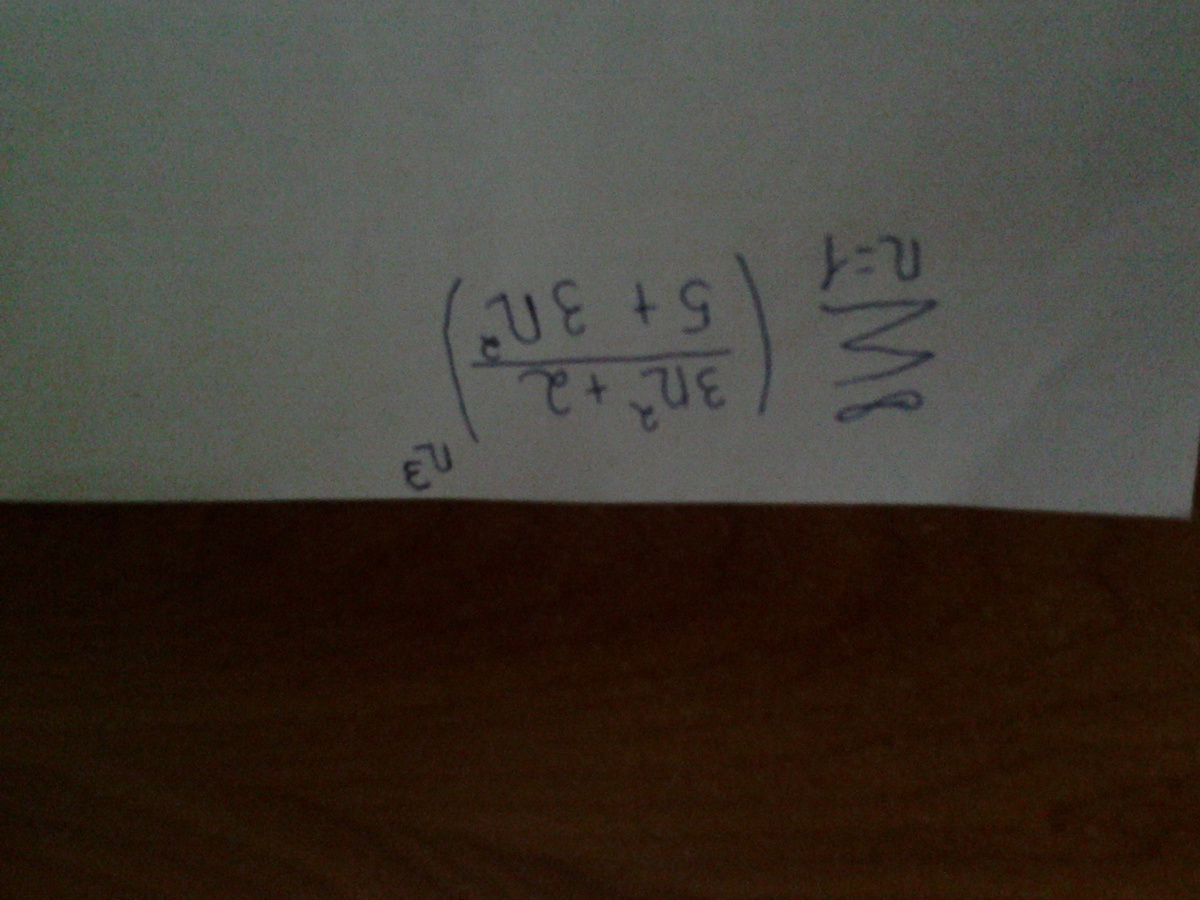Ответы
Ответ дал:
0
Применяем радикальный признак Коши
![lim_{n to infty} sqrt[n]{a_n}= lim_{n to infty} sqrt[n]{ (frac{3n ^{2}+2 }{5+3n^{2} }) ^{n ^{3} } } = \ =lim_{n to infty} ((1-frac{3}{5+3n ^{2} }) ^{ -frac{5+3n^{2} }{-3} } ) ^{ frac{-3n^{2} }{5+3n ^{2} } }=e ^{ lim_{n to infty} frac{-3n ^{2} }{5+3n ^{2} } }=e ^{-1}= frac{1}{e}<1 lim_{n to infty} sqrt[n]{a_n}= lim_{n to infty} sqrt[n]{ (frac{3n ^{2}+2 }{5+3n^{2} }) ^{n ^{3} } } = \ =lim_{n to infty} ((1-frac{3}{5+3n ^{2} }) ^{ -frac{5+3n^{2} }{-3} } ) ^{ frac{-3n^{2} }{5+3n ^{2} } }=e ^{ lim_{n to infty} frac{-3n ^{2} }{5+3n ^{2} } }=e ^{-1}= frac{1}{e}<1](https://tex.z-dn.net/?f=+lim_%7Bn+to+infty%7D++sqrt%5Bn%5D%7Ba_n%7D%3D+lim_%7Bn+to+infty%7D++sqrt%5Bn%5D%7B+%28frac%7B3n+%5E%7B2%7D%2B2+%7D%7B5%2B3n%5E%7B2%7D+%7D%29+%5E%7Bn+%5E%7B3%7D+%7D+%7D+%3D++%5C+%3Dlim_%7Bn+to+infty%7D+%28%281-frac%7B3%7D%7B5%2B3n+%5E%7B2%7D+%7D%29+%5E%7B+-frac%7B5%2B3n%5E%7B2%7D+%7D%7B-3%7D+%7D+%29+%5E%7B+frac%7B-3n%5E%7B2%7D+%7D%7B5%2B3n+%5E%7B2%7D+%7D+%7D%3De+%5E%7B+lim_%7Bn+to+infty%7D+frac%7B-3n+%5E%7B2%7D+%7D%7B5%2B3n+%5E%7B2%7D+%7D++%7D%3De+%5E%7B-1%7D%3D+frac%7B1%7D%7Be%7D%26lt%3B1++++++)
Так как предел имеет значение <1, то согласно признака ряд сходится.
Так как предел имеет значение <1, то согласно признака ряд сходится.
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад